题目内容
16. 匀质铁链悬挂在天花板上,其中A点是最低点.C点是悬挂点,B点是介于A、C之间的某一点,关于这三点铁链张力大小,下列说法正确的是( )
匀质铁链悬挂在天花板上,其中A点是最低点.C点是悬挂点,B点是介于A、C之间的某一点,关于这三点铁链张力大小,下列说法正确的是( )| A. | A点的张力最大 | |
| B. | C点的张力最大 | |
| C. | A、B、C三点张力大小均相等 | |
| D. | 铁链C处切线方向有可能是竖直方向 |
分析 对AC铁链受力分析,受重力、左侧的铁链对其向左的拉力,天花板的拉力,根据平衡条件列式求解铁链在A、C处弹力大小.同理求出B点的拉力,然后比较即可.
解答 解:设AC段铁链的质量为m,对AC段受力分析,受重力、左侧的铁链对其向左的拉力,天花板的拉力,如图所示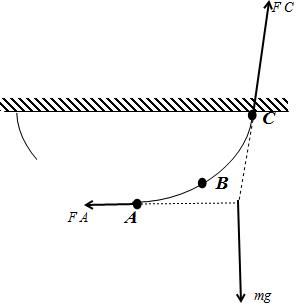
根据平衡条件和受力关系,有:${F}_{C}=\sqrt{{F}_{A}^{2}+{m}^{2}{g}^{2}}$
可知C点的拉力大于A点的拉力
再以AB段为研究对象,如图,由于AB段铁链的质量小于AC段的质量,则: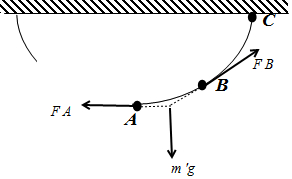
${F}_{B}^{\;}=\sqrt{{F}_{A}^{2}+{m′}^{2}{g}^{2}}<{F}_{C}$=$\sqrt{{F}_{A}^{2}+{m}^{2}{g}^{2}}$
所以A、B、C三点张力大小关系为A点最小,C点最大,而且A点的张力的方向沿水平方向.
故只有B正确,ACD错误
故选:B
点评 本题考查共点力的平衡条件以及隔离法的应用,解答的关键是能够灵活地选择研究对象,然后运用平衡条件列式求解即可.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
6. 电梯内放置一木块,已知木块的重力大小为G,电梯地板对木块的支持力大小为N,木块对电梯地板的压力大小为N′,支持力和压力的方向如图所示.现在电梯加速上升,则( )
电梯内放置一木块,已知木块的重力大小为G,电梯地板对木块的支持力大小为N,木块对电梯地板的压力大小为N′,支持力和压力的方向如图所示.现在电梯加速上升,则( )
 电梯内放置一木块,已知木块的重力大小为G,电梯地板对木块的支持力大小为N,木块对电梯地板的压力大小为N′,支持力和压力的方向如图所示.现在电梯加速上升,则( )
电梯内放置一木块,已知木块的重力大小为G,电梯地板对木块的支持力大小为N,木块对电梯地板的压力大小为N′,支持力和压力的方向如图所示.现在电梯加速上升,则( )| A. | N=N′>G | B. | N>N′>G | ||
| C. | 木块处于超重状态 | D. | 木块处于失重状态 |
7.设地球对地面上某物体的万有引力大小为F1,该物体对地球的万有引力大小为F2,则( )
| A. | F1大于F2 | B. | F1小于F2 | ||
| C. | F1等于F2 | D. | F1可能大于F2,也可能小于F2 |
4. 如图所示,在光滑水平面上有两枚钉子,一枚钉上系一轻绳,绳的另一端系一小球,绳拉紧时绳与两钉恰在一直线上.现给小球一个垂直于绳的水平速度,小球绕钉转动,转过半圈时绳与另一钉子相碰,以后线逐渐绕到钉上,则小球每转过半圈其( )
如图所示,在光滑水平面上有两枚钉子,一枚钉上系一轻绳,绳的另一端系一小球,绳拉紧时绳与两钉恰在一直线上.现给小球一个垂直于绳的水平速度,小球绕钉转动,转过半圈时绳与另一钉子相碰,以后线逐渐绕到钉上,则小球每转过半圈其( )
 如图所示,在光滑水平面上有两枚钉子,一枚钉上系一轻绳,绳的另一端系一小球,绳拉紧时绳与两钉恰在一直线上.现给小球一个垂直于绳的水平速度,小球绕钉转动,转过半圈时绳与另一钉子相碰,以后线逐渐绕到钉上,则小球每转过半圈其( )
如图所示,在光滑水平面上有两枚钉子,一枚钉上系一轻绳,绳的另一端系一小球,绳拉紧时绳与两钉恰在一直线上.现给小球一个垂直于绳的水平速度,小球绕钉转动,转过半圈时绳与另一钉子相碰,以后线逐渐绕到钉上,则小球每转过半圈其( )| A. | 线速度变小一次 | B. | 角速度变大一次 | ||
| C. | 向心加速度变小一次 | D. | 向心力变大一次 |
11.解决物理疑难问题的过程,往往伴随新理论的建立,在物理学史中,下列现象与物理新理论的建立不存在必然联系的是( )
| A. | 行星绕太阳运动与万有引力 | B. | 电荷间作用力与电场 | ||
| C. | 光电效应现象与光子说 | D. | 氢原子光谱与质能方程 |
1.已知氢原子的基态能量为E1,激发态能量为En=$\frac{{E}_{1}}{{n}^{2}}$,其中n=2,3,4….1885年,巴尔末对当时已知的在可见光区的四条谱线做了分析,发现这些谱线的波长能够用一个公式表示,这个公式写做$\frac{1}{λ}=R({\frac{1}{2^2}-\frac{1}{n^2}})$,n=3,4,5,….式中R叫做里德伯常量,这个公式称为巴尔末公式.用h表示普朗克常量,c表示真空中的光速,则里德伯常量R可以表示为( )
| A. | $-\frac{E_1}{hc}$ | B. | $\frac{E_1}{2hc}$ | C. | $-\frac{E_1}{2hc}$ | D. | $\frac{E_1}{hc}$ |
5.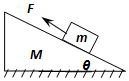 如图所示,质量为M的楔形物块静置在粗糙水平地面上,其斜面的倾角为θ.斜面上有一质量为m的小物块,小物块与斜面之间存在摩擦. 用恒力F沿斜面向上拉小物块,使之匀速上滑.在小物块运动的过程中,楔形物块始终保持静止.( )
如图所示,质量为M的楔形物块静置在粗糙水平地面上,其斜面的倾角为θ.斜面上有一质量为m的小物块,小物块与斜面之间存在摩擦. 用恒力F沿斜面向上拉小物块,使之匀速上滑.在小物块运动的过程中,楔形物块始终保持静止.( )
 如图所示,质量为M的楔形物块静置在粗糙水平地面上,其斜面的倾角为θ.斜面上有一质量为m的小物块,小物块与斜面之间存在摩擦. 用恒力F沿斜面向上拉小物块,使之匀速上滑.在小物块运动的过程中,楔形物块始终保持静止.( )
如图所示,质量为M的楔形物块静置在粗糙水平地面上,其斜面的倾角为θ.斜面上有一质量为m的小物块,小物块与斜面之间存在摩擦. 用恒力F沿斜面向上拉小物块,使之匀速上滑.在小物块运动的过程中,楔形物块始终保持静止.( )| A. | 地面对楔形物块的支持力为(M+m)g | |
| B. | 地面对楔形物块的支持力为(M+m)g-Fsinθ | |
| C. | 楔形物块对小物块的摩擦力一定为mgsinθ | |
| D. | 楔形物块对小物块的支持力一定为mgsinθ |
12.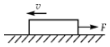 如图所示,重为10N的物体以速度v 在粗糙的水平面上向左运动,物体与桌面间的动摩擦因数为0.2.现在给物体施加水平向右的拉力F,其大小为18N,则物体受到的摩擦力和加速度大小为(g 取10m/s2)( )
如图所示,重为10N的物体以速度v 在粗糙的水平面上向左运动,物体与桌面间的动摩擦因数为0.2.现在给物体施加水平向右的拉力F,其大小为18N,则物体受到的摩擦力和加速度大小为(g 取10m/s2)( )
 如图所示,重为10N的物体以速度v 在粗糙的水平面上向左运动,物体与桌面间的动摩擦因数为0.2.现在给物体施加水平向右的拉力F,其大小为18N,则物体受到的摩擦力和加速度大小为(g 取10m/s2)( )
如图所示,重为10N的物体以速度v 在粗糙的水平面上向左运动,物体与桌面间的动摩擦因数为0.2.现在给物体施加水平向右的拉力F,其大小为18N,则物体受到的摩擦力和加速度大小为(g 取10m/s2)( )| A. | 2N,20m/s2 | B. | 0,21m/s2 | C. | 1N,21m/s2 | D. | 2N,18m/s2 |
