题目内容
14.汽车前方20m处有一自行车正以8m/s的速度匀速前进,汽车从静止开始以2m/s2的加速度追赶自行车,若两车在同一条公路不同车道上做同方向的直线运动,求:(1)经多长时间,两车第一次相遇?
(2)若汽车追上自行车后立即刹车,汽车刹车过程中的加速度大小为2m/s2,则再经多长时间两车第二次相遇?
分析 (1)根据位移关系,结合运动学公式求出第一次相遇的时间.
(2)根据速度时间公式求出减速时的初速度,根据速度时间公式求出汽车速度减为零的时间,分别求出此时汽车和自行车的位移,判断出自行车没有追上汽车,再结合位移关系求出继续追及的时间,从而得出第二次相遇的时间.
解答 解:(1)第一次相遇时,根据位移关系有:$\frac{1}{2}{a_1}{t_1}^2-{v_自}{t_1}=20$
代入数据解得t1=10s.
(2)汽车减速的初速度v车=a1t1=2×10m/s=20m/s,
则汽车停下来所用时间${t}_{2}=\frac{{v}_{车}}{{a}_{2}}=\frac{20}{2}s=10s$,
汽车位移${x}_{车}=\frac{{v}_{车}}{2}{t}_{2}=\frac{20}{2}×10m=100m$,
此过程中自行车位移x自=v自t2=8×10m=80m
即自行车此时未追上汽车,还需要的时间为${t_3}=\frac{{{x_车}-{x_自}}}{v_自}=\frac{20}{8}=2.5s$
即t总=t2+t3=12.5s.
答:(1)经10s时间,两车第一次相遇.
(2)再经12.5s时间两车第二次相遇.
点评 解决本题的关键知道两车相遇位移具有一定的关系.注意第二次相遇要判断汽车是否停止,不能死代公式.

练习册系列答案
相关题目
5.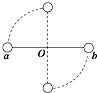 如图所示,在两个质量分别为m、2m的小球a和b之间,用一根长为L的轻杆连接(杆的质量可不计),两小球可绕着轻杆中心O的水平轴无摩擦转动.现让轻杆处于水平位置,然后无初速度释放,重球b向下运动,轻球a向上运动,产生转动,在杆转至竖直的过程中( )
如图所示,在两个质量分别为m、2m的小球a和b之间,用一根长为L的轻杆连接(杆的质量可不计),两小球可绕着轻杆中心O的水平轴无摩擦转动.现让轻杆处于水平位置,然后无初速度释放,重球b向下运动,轻球a向上运动,产生转动,在杆转至竖直的过程中( )
 如图所示,在两个质量分别为m、2m的小球a和b之间,用一根长为L的轻杆连接(杆的质量可不计),两小球可绕着轻杆中心O的水平轴无摩擦转动.现让轻杆处于水平位置,然后无初速度释放,重球b向下运动,轻球a向上运动,产生转动,在杆转至竖直的过程中( )
如图所示,在两个质量分别为m、2m的小球a和b之间,用一根长为L的轻杆连接(杆的质量可不计),两小球可绕着轻杆中心O的水平轴无摩擦转动.现让轻杆处于水平位置,然后无初速度释放,重球b向下运动,轻球a向上运动,产生转动,在杆转至竖直的过程中( )| A. | b球的重力势能减小量与其动能增大量相等 | |
| B. | a球的重力势能增大,动能减小 | |
| C. | 杆对a球做正功和杆对b球做的负功代数和为零 | |
| D. | a球和b球的总重力势能不变化 |
19.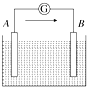 如图所示是一种化学原电池,电路中的电流表可以测定电流的方向,测得外电路的电流方向如图所示.其中两金属板分别为锌板和铜板,电解槽中的电解液为硫酸铜.下列说法中不正确的是( )
如图所示是一种化学原电池,电路中的电流表可以测定电流的方向,测得外电路的电流方向如图所示.其中两金属板分别为锌板和铜板,电解槽中的电解液为硫酸铜.下列说法中不正确的是( )
 如图所示是一种化学原电池,电路中的电流表可以测定电流的方向,测得外电路的电流方向如图所示.其中两金属板分别为锌板和铜板,电解槽中的电解液为硫酸铜.下列说法中不正确的是( )
如图所示是一种化学原电池,电路中的电流表可以测定电流的方向,测得外电路的电流方向如图所示.其中两金属板分别为锌板和铜板,电解槽中的电解液为硫酸铜.下列说法中不正确的是( )| A. | A是铜板,B是锌板 | |
| B. | A是锌板,B是铜板 | |
| C. | A端是电源的正极,B端是电源的负极 | |
| D. | 该种电池能把化学能转化为电能 |
6.物体做匀变速直线运动,已知在时间t内通过的位移为x,则以下说法正确的是( )
| A. | 可求出物体在时间t内的平均速度 | |
| B. | 可求出物体的加速度 | |
| C. | 可求出物体在这段时间内中间时刻的瞬时速度 | |
| D. | 可求出物体通过$\frac{x}{2}$时的速度 |

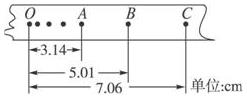 在“验证机械能守恒定律”的实验中,打点计时器所用电源频率为50 Hz,当地重力加速度的值为9.80 m/s2,测得所用重物的质量为1.00 kg.
在“验证机械能守恒定律”的实验中,打点计时器所用电源频率为50 Hz,当地重力加速度的值为9.80 m/s2,测得所用重物的质量为1.00 kg.