Question

【题目】如图所示，平静湖面岸边的垂钓者的眼睛恰好位于岸边P点正上方h1=0.6m高度处，浮标Q离P点s1=0.8m远，PQ水平，鱼饵灯M在浮标的正前方s2=1.2m处的水下，垂钓者发现鱼饵灯刚好被浮标挡住，已知水的折射率n=光在真空中的速度 c=3×108m/s，求

（1）鱼饵灯离水面的深度h2

（2）光线在水中传播的时间t.

Answer 1

【答案】(1)1.6m (2)

【解析】试题分析：作出光路图，由几何知识得出入射角的正弦值与折射角的正弦值表达式，再结合折射定律求鱼饵灯离水面的深度h2；根据求出光在水中的传播速度，由几何知识求出光在水中传播的距离，即可求得传播时间。

设光线从水中射入空气中的折射角和入射角分别为i、r

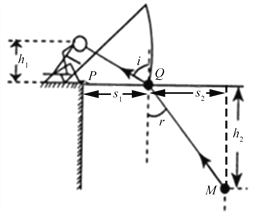
则有：

根据光的折射定律可知：

联立并代入数据得，鱼饵灯离水面的深度：h2=1.6 m

②光线在水中传播的距离为：

根据公式

可得光线在水中传播的时间：