��Ŀ����
����Ŀ����ͼ��λ����ֱƽ���ڵĹ⻬������ķ�֮һԲ��ab��������bc��ɣ�Բ���뾶Oaˮƽ��b��Ϊ�����߶��㣮��֪h=2m��s= ![]() m��ȡ�������ٶȴ�Сg=10m/s2 ��
m��ȡ�������ٶȴ�Сg=10m/s2 �� 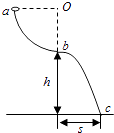
��1��һС�����ڹ���ϴ�a���ɾ�ֹ���£�������bc�ι���˶�ʱ������֮���������������Բ������İ뾶��
��2��������b���ɾ�ֹ��С�Ŷ�����ʼ���£�����c��ʱ�ٶȵ�ˮƽ�����Ĵ�С��
���𰸡�
��1��
�⣺������bc�ι���˶�ʱ������֮�����������������bc��ֻ����������ƽ���˶������У�
![]() =
= ![]() ��
��
����b����ٶ� ![]() �ڣ�
�ڣ�
��a��b�Ĺ����У����ݶ��ܶ����ã�
![]() ��
��
��ã�R=0.25m��
��2��
�⣺��b���»������У����ٶ�Ϊ�㣬ֻ������������b��c�Ĺ����У����ݶ��ܶ����ã�
![]() ��
��
��Ϊ���廬��c��ʱ����ֱ����ļнǵ��ڣ�1��������ƽ���˶������о���c��ʱ�ٶ�����ֱ����ļн���ȣ���Ϊ�ȣ�
�����ƽ���˶����ɿ�֪ ![]() �ݣ�
�ݣ�
�����˶��ĺϳ���ֽ�ɵ� ![]() ��
��
�ɢ٢ڢۢܢݢ�ã�vˮƽ= ![]() m/s
m/s
����������1��������bc�ι���˶�ʱ������֮�����������������bc��ֻ����������ƽ���˶�������ƽ���˶�������ʽ���b���ٶȣ��ٸ��ݶ��ܶ������R����2���»������У����ٶ�Ϊ�㣬ֻ������������b��c�Ĺ����У����ݶ��ܶ�����ʽ������ƽ���˶�������ʽ���c���ٶȷ�������ֱ����ļнǣ��ٽ���˶��ĺϳ���ֽ���⣮

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ��ijͬѧ����ͼ��a����ʾ��·�������������ʱ�������ĵ�ѹ��ʱ��ı仯��ʵ����ʹ�õ�����Ϊ�����E�������С��������S1��S2��������C��Լ100��F��������R1��Լ200k����������R2��1k��������ѹ�� ![]() ������6V����������������ɣ�
������6V����������������ɣ�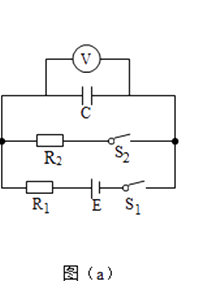
��1����ͼ��a����ʾ�ĵ�·ԭ��ͼ��ͼ��b����ʵ��ͼ���ߣ�
��2���ȱպϿ���S2 �� �ٶϿ�����S2���պϿ���S1 �� ͬʱ���������ʼ��ʱ����ijʱ�̵�ѹ����ʾ����ͼ��c����ʾ����ѹ���Ķ���ΪV������2λС������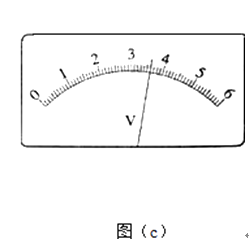
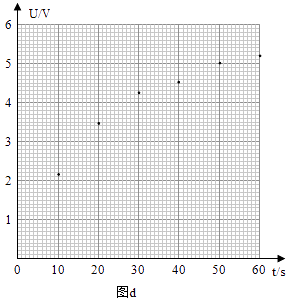
��3����ͬѧÿ��10s��¼һ�ε�ѹ���Ķ���U����¼�����������ʾ����ͼ��d������������ֽ�ϻ��U��tͼ�� �� ��ֻ֪��һ�����ݵ����ϴ����ݵ��Ӧ�ı��е�ʱ����s��
ʱ��t/s | 10.0 | 20.0 | 30.0 | 40.0 | 50.0 | 60.0 |
��ѹU/V | 2.14 | 3.45 | 4.23 | 4.51 | 5.00 | 5.18 |
��4����·��C��R2��S2���ɵĻ�·�������� ��
����Ŀ����ͼ��ʾ����̽������������ɡ���ʵ���У����ν���ȼ�����������������ڹ�����ϣ��������桢�������������Ĵ�����ͬһ�߶ȣ�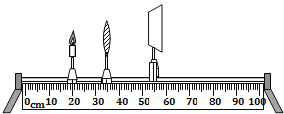
�����С��ͬѧʵ��ʱ��¼�ļ������ݣ�
ʵ����� | ���u/cm | ���v/cm |
1 | 30 | 15 |
2 | 20 | 20 |
3 | 15 | 30 |
4 | 5 | / |
��1����4��ʵ��ʱ��������ص��ǣ�
��2���������ϵõ�һ��������С��ʵ��ʱ����������λ�ò��䣬Ҫʹ���ϵ�����Щ��Ӧ������������������������������������������
��3����1��ʵ��ʱ��С����һ�����۾�����������ǰ�棬Ҫ�ڹ������ٴεõ���������Ӧ�������������������ƶ���