��Ŀ����
����Ŀ����ͼ��ʾ��һ����M=2kg�Ĵ��л��ι����ƽ̨�����㹻����ˮƽ����ϣ����ι����ˮƽ���ƽ�����ӣ�ˮƽ����Ͼ���һС��B �� �ӻ��ι���Ͼ���ˮƽ�����h=0.3m���ɾ�ֹ�ͷ�һ����mA=1kg��С��A �� С��A�ع���»�����С��B������������������С��A�����أ���ǡ������ƽ̨����֪���нӴ�����⻬���������ٶ�Ϊg �� ��С��B��������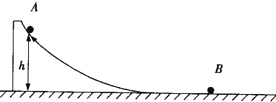
���𰸡���С��A�»���ˮƽ�����ʱ���ٶȴ�СΪv1 �� ƽ̨ˮƽ�ٶȴ�СΪv �� ������Ϊ�������ɶ����غ㶨���У�
mAv1=Mv
�������غ㶨���У�
mAgh= ![]() mAv12+
mAv12+ ![]() mBv22
mBv22
�������������ݽ�ã�
v1=2m/s ��
v=1m/s
С��A��B�����˶������෴����С��A��B���ٶȴ�С�ֱ�Ϊv1���v2 �� ������֪��
v1��=1m/s
�ɶ����غ㶨�ɵã�
mAv1=��mAv1��+mBv2
�������غ㶨���У�![]() mAv12=
mAv12= ![]() mAv12+
mAv12+ ![]() mBv22
mBv22
�������������ݽ�ã�mB=3kg
��������С��A��ƽ̨�����������ܶ����غ㣬�ɶ����غ���ʽ�����ɹ��ܹ�ϵ��ʽ����С��A��ƽ̨���ٶȣ��ٶ�С���B���з������ɶ����غ�ͻ�е���غ�����������B���������
�����㾫����������Ҫ�����˶����غ㶨�ɵ����֪ʶ�㣬��Ҫ���ն����غ㶨�ɳ�����������ϵͳ����������ϵͳ���������ĺ���Ϊ�㣻ϵͳ���ܵ������ĺ����䲻Ϊ�㣬��ϵͳ����������С�öࣻϵͳ���������ĺ����䲻Ϊ�㣬����ij�������ϵķ���Ϊ�㣬���ڸ÷�����ϵͳ���ܶ����ķ������ֲ��������ȷ�����⣮