题目内容
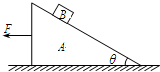 在水平面上放置一倾角为θ的斜面体A,质量为M,与水平面间动摩擦因数为μ1,在其斜面上静放一质量为m的物块B,A、B间动摩擦因数为μ2(已知μ2>tanθ),如图所示.现将一水平向左的力F作用在斜面体A上,F的数值由零逐渐增加,当A、B将要发生相对滑动时,F不再改变,设滑动摩擦力等于最大静摩擦力.求:
在水平面上放置一倾角为θ的斜面体A,质量为M,与水平面间动摩擦因数为μ1,在其斜面上静放一质量为m的物块B,A、B间动摩擦因数为μ2(已知μ2>tanθ),如图所示.现将一水平向左的力F作用在斜面体A上,F的数值由零逐渐增加,当A、B将要发生相对滑动时,F不再改变,设滑动摩擦力等于最大静摩擦力.求:(1)B所受摩擦力的最大值;
(2)水平力F的最大值;
(3)定性画出整个过程中AB的速度随时间变化的图象.
分析:(1)隔离对B分析,结合竖直方向上的合力为零,求出B所受摩擦力的最大值.
(2)对B运用正交分解,结合水平方向上的合力求出B的加速度,通过B与整体的加速度相等,对整体分析,运用牛顿第二定律求出水平力F的最大值.
(3)AB开始在拉力较小时,保持静止,运动后,F增大,做加速度增大的加速运动,AB相对滑动后,F保持不变,做匀加速直线运动.
(2)对B运用正交分解,结合水平方向上的合力求出B的加速度,通过B与整体的加速度相等,对整体分析,运用牛顿第二定律求出水平力F的最大值.
(3)AB开始在拉力较小时,保持静止,运动后,F增大,做加速度增大的加速运动,AB相对滑动后,F保持不变,做匀加速直线运动.
解答:解:(1)B受力如图所示.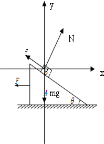
B在竖直方向上平衡,有:fsinθ+Ncosθ=mg ①
又f=μ2N ②
联立①②两式解得f=
. ③
(2)B与整体具有相同的加速度.
对B分析,在水平方向上有:fcosθ-Nsinθ=ma ④
对整体分析,F-μ1(m+M)g=(M+m)a ⑤
联立③④⑤解得F=(M+m)g(μ1+
).
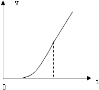
(3)在开始阶段,F较小时,AB处于静止状态,然后AB一起做加速度越来越大的加速运动,AB发生相对滑动后,F不变,做匀加速直线运动.
速度时间图线如图所示.
 答:(1)B所受摩擦力的最大值f=
答:(1)B所受摩擦力的最大值f=
.
(2)水平力F的最大值F=(M+m)g(μ1+
).
(3)如图所示.

B在竖直方向上平衡,有:fsinθ+Ncosθ=mg ①
又f=μ2N ②
联立①②两式解得f=
| μ2mg |
| μ2sinθ+cosθ |
(2)B与整体具有相同的加速度.
对B分析,在水平方向上有:fcosθ-Nsinθ=ma ④
对整体分析,F-μ1(m+M)g=(M+m)a ⑤
联立③④⑤解得F=(M+m)g(μ1+
| μ2cosθ-sinθ |
| μ2sinθ+cosθ |
(3)在开始阶段,F较小时,AB处于静止状态,然后AB一起做加速度越来越大的加速运动,AB发生相对滑动后,F不变,做匀加速直线运动.
速度时间图线如图所示.
 答:(1)B所受摩擦力的最大值f=
答:(1)B所受摩擦力的最大值f=| μ2mg |
| μ2sinθ+cosθ |
(2)水平力F的最大值F=(M+m)g(μ1+
| μ2cosθ-sinθ |
| μ2sinθ+cosθ |
(3)如图所示.
点评:解决本题的关键能够正确地受力分析,运用牛顿第二定律进行求解,知道AB保持相对静止时,具有相同的加速度.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目



