题目内容
(10分)在水平面上放置一倾角为θ的斜面体A,质量为M,与水平面间动摩擦因数为μ1,在其斜面上静放一质量为m的物块B,A、B间动摩擦因数为μ2(已知μ2>tanθ),如图所示。现将一水平向左的力F作用在斜面体A上, F的数值由零逐渐增加,当A、B将要发生相对滑动时,F不再改变。设滑动摩擦力等于最大静摩擦力。求:

(1)B所受摩擦力的最大值;
(2)水平力F的最大值;
(3)定性画出整个过程中AB的速度随时间变化的图象。
(1) (2) (μ1+
(2) (μ1+
 )
(M+m)g (3)如下图。
)
(M+m)g (3)如下图。


【解析】(1)A、B先静止,后做加速度不断增加的加速运动,最后做匀加速直线运动,此时A对B有最大摩擦力。物块A受力如图,设最大加速度为a,
在x轴方向由牛顿第二定律得Ff cosθ- FN sinθ = ma ① (1分)
在y轴方向由平衡条件得 Ff sinθ+ FN cosθ = mg ② (1分)
又 Ff = μ2FN ③ (1分)
由①②③得
Ff =  ④
(2分)
④
(2分)
(2)由以上各式得a =  g
⑤
(2分)
g
⑤
(2分)
A、B的加速度均为a,由牛顿第二定律得F –μ1(M+m)g = (M+m)a ⑥
由⑤⑥得F = (μ1+  ) (M+m)g ⑦
(2分)
) (M+m)g ⑦
(2分)

(3)如下图。 (3分)

本题考查牛顿第二定律的应用,A、B先静止,后做加速度不断增加的加速运动,最后做匀加速直线运动,根据牛顿第二定律对两个过程列式,联立求解,以整体为研究对象,根据牛顿第二定律列公式求解

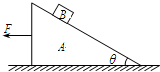 在水平面上放置一倾角为θ的斜面体A,质量为M,与水平面间动摩擦因数为μ1,在其斜面上静放一质量为m的物块B,A、B间动摩擦因数为μ2(已知μ2>tanθ),如图所示.现将一水平向左的力F作用在斜面体A上,F的数值由零逐渐增加,当A、B将要发生相对滑动时,F不再改变,设滑动摩擦力等于最大静摩擦力.求:
在水平面上放置一倾角为θ的斜面体A,质量为M,与水平面间动摩擦因数为μ1,在其斜面上静放一质量为m的物块B,A、B间动摩擦因数为μ2(已知μ2>tanθ),如图所示.现将一水平向左的力F作用在斜面体A上,F的数值由零逐渐增加,当A、B将要发生相对滑动时,F不再改变,设滑动摩擦力等于最大静摩擦力.求:

