题目内容
2.2015年4月1日,中国首次公开登月飞船方案.两种飞船中,全重20吨的飞船可支持登月任务.(1)已知地球半径为R,地球表面的重力加速度为g,月球绕地球运动的轨道半径r,月球绕地球的运动近似看做匀速圆周运动,求月球绕地球运动的周期为T.
(2)若宇航员随登月飞船登陆月球后,站在月球表面从高h处以速度v0水平抛出一小球,经过时间t,小球落地.已知月球半径为r月,引力常量为G,求月球的密度ρ月.
分析 (1)根据万有引力提供向心力,结合万有引力等于重力,列式求出月球绕地球运动的周期为T.
(2)小球做平抛运动,分位移公式可求得月球表面的重力加速度g,忽略月球自转的影响,根据万有引力等于重力列出等式求解月球质量,从而算出月球的密度;
解答 解:(1)设地球的质量为M,根据万有引力定律和牛顿第二定律得:
G$\frac{M{M}_{月}}{{r}^{2}}$=M月($\frac{2π}{T}$)2r
质量为m的物体在地球表面时:
mg=G$\frac{Mm}{{R}^{2}}$
解得:
T=2π$\sqrt{\frac{{r}^{3}}{g{R}^{2}}}$
(2)设月球表面处的重力加速度为g月,对平抛运动,根据分位移公式,有:
h=$\frac{1}{2}{g}_{月}{t}^{2}$
解得:
${g}_{月}=\frac{2h}{{t}^{2}}$
在月球表面上,小球所受重力等于月球对小球的吸引力,故:
mg月=G$\frac{{M}_{月}m}{{r}_{月}^{2}}$
月球的密度:
${ρ}_{月}=\frac{{M}_{月}}{\frac{4}{3}π{r}_{月}^{2}}$
联立解得:
${ρ}_{月}=\frac{3h}{2π{r}_{月}G{t}^{2}}$
答:(1)月球绕地球运动的周期为2π$\sqrt{\frac{{r}^{3}}{g{R}^{2}}}$;
(2)月球的密度为$\frac{3h}{2π{r}_{月}G{t}^{2}}$.
点评 解决本题的关键掌握万有引力定律的两个重要理论:1、万有引力提供向心力,2、万有引力等于重力.并能灵活运用;重力加速度g是天体运动研究和天体表面宏观物体运动研究联系的物理量.

练习册系列答案
相关题目
1.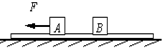 一个质量可忽略不计的长轻质木板置于光滑水平地面上,木板上放质量分别为mA=1kg和mB=2kg的A、B两物块,A、B与木板之间的动摩擦因数都为μ=0.2,水平恒力F作用在A物块上,如图所示(重力加速度g取10m/s2).则下列说法正确的是( )
一个质量可忽略不计的长轻质木板置于光滑水平地面上,木板上放质量分别为mA=1kg和mB=2kg的A、B两物块,A、B与木板之间的动摩擦因数都为μ=0.2,水平恒力F作用在A物块上,如图所示(重力加速度g取10m/s2).则下列说法正确的是( )
 一个质量可忽略不计的长轻质木板置于光滑水平地面上,木板上放质量分别为mA=1kg和mB=2kg的A、B两物块,A、B与木板之间的动摩擦因数都为μ=0.2,水平恒力F作用在A物块上,如图所示(重力加速度g取10m/s2).则下列说法正确的是( )
一个质量可忽略不计的长轻质木板置于光滑水平地面上,木板上放质量分别为mA=1kg和mB=2kg的A、B两物块,A、B与木板之间的动摩擦因数都为μ=0.2,水平恒力F作用在A物块上,如图所示(重力加速度g取10m/s2).则下列说法正确的是( )| A. | 若F=1N,则A、B都相对板静止不动 | |
| B. | 若F=1.5N,则A物块所受摩擦力大小为1.5N | |
| C. | 若F=4N,则B物块所受摩擦力大小为4N | |
| D. | 若F=6N,则B物块的加速度为1m/s2 |
2.如图所示,水平板上有质量为m=1.0kg的物块,受到随时间t变化的水平拉力F作用,用力传感器测出相应时物块所受摩擦力Ff的大小.g取10N/kg,则下列判断正确的是( )

| A. | 5s内拉力对物块做功为零 | |
| B. | 4s末物块所受力不平衡 | |
| C. | 物块与木板之间的摩擦力大小是一个定值 | |
| D. | 物块先处于静止状态,后做匀速运动 |
10.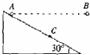 如图所示,位于同一高度的小球A、B分别以v1和v2的速度水平抛出,都落在了倾角为30°的斜面上的C点,小球B恰好垂直打到斜面上,则v1,v2大小之比为( )
如图所示,位于同一高度的小球A、B分别以v1和v2的速度水平抛出,都落在了倾角为30°的斜面上的C点,小球B恰好垂直打到斜面上,则v1,v2大小之比为( )
 如图所示,位于同一高度的小球A、B分别以v1和v2的速度水平抛出,都落在了倾角为30°的斜面上的C点,小球B恰好垂直打到斜面上,则v1,v2大小之比为( )
如图所示,位于同一高度的小球A、B分别以v1和v2的速度水平抛出,都落在了倾角为30°的斜面上的C点,小球B恰好垂直打到斜面上,则v1,v2大小之比为( )| A. | 2:1 | B. | 3:2 | C. | 2:3 | D. | 4:3 |
7.下列光学现象的说法正确的是( )
| A. | 在水中绿光的传播速度比红光的小 | |
| B. | 光纤由内芯和外套两层组成,内芯的折射率比外套的小 | |
| C. | 在岸边观察水中的鱼,看到的深度比实际的深 | |
| D. | 分别用绿光和红光在同一装置上做双缝干涉实验,用红光时得到的条纹间距更窄 |
14.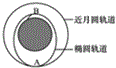 我国研制的“嫦娥三号”月球探测器于2013年12月1日发射成功,并成功在月球表面实现软着陆.探测器首先被送到距离月球表面高度为H的近月轨道做匀速圆周运动,之后在轨道上的A点实施变轨,使探测器绕月球做椭圆运动,当运动到B点时继续运动,探测器携带的传感器测得自由落体运动时间为t,已知月球半径为R,万有引力常量为G.则下列正确的是( )
我国研制的“嫦娥三号”月球探测器于2013年12月1日发射成功,并成功在月球表面实现软着陆.探测器首先被送到距离月球表面高度为H的近月轨道做匀速圆周运动,之后在轨道上的A点实施变轨,使探测器绕月球做椭圆运动,当运动到B点时继续运动,探测器携带的传感器测得自由落体运动时间为t,已知月球半径为R,万有引力常量为G.则下列正确的是( )
 我国研制的“嫦娥三号”月球探测器于2013年12月1日发射成功,并成功在月球表面实现软着陆.探测器首先被送到距离月球表面高度为H的近月轨道做匀速圆周运动,之后在轨道上的A点实施变轨,使探测器绕月球做椭圆运动,当运动到B点时继续运动,探测器携带的传感器测得自由落体运动时间为t,已知月球半径为R,万有引力常量为G.则下列正确的是( )
我国研制的“嫦娥三号”月球探测器于2013年12月1日发射成功,并成功在月球表面实现软着陆.探测器首先被送到距离月球表面高度为H的近月轨道做匀速圆周运动,之后在轨道上的A点实施变轨,使探测器绕月球做椭圆运动,当运动到B点时继续运动,探测器携带的传感器测得自由落体运动时间为t,已知月球半径为R,万有引力常量为G.则下列正确的是( )| A. | “嫦娥三号”的发射速度必须大于第一宇宙速度 | |
| B. | 探测器在近月轨道和椭圆轨道上的周期相等 | |
| C. | “嫦娥三号”在A点变轨时,需减速才能从近月圆轨道进入椭圆轨道 | |
| D. | 月球的平均密度为$\frac{3h}{2πGR{t}^{2}}$ |
12.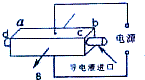 电磁泵在目前的生产科技中得到了广泛应用.如图所示是电磁泵的原理图,泵体是一个长方体,ab边长为L,两侧端面是边长为a的正方形;流经泵体内的液体密度为ρ,在进口处接入电导率为σ(电阻率的倒数)的导电液,泵体所在处有方向垂直侧面向外的磁场B,泵体的上下两表面接在电压恒为U的电源上.则( )
电磁泵在目前的生产科技中得到了广泛应用.如图所示是电磁泵的原理图,泵体是一个长方体,ab边长为L,两侧端面是边长为a的正方形;流经泵体内的液体密度为ρ,在进口处接入电导率为σ(电阻率的倒数)的导电液,泵体所在处有方向垂直侧面向外的磁场B,泵体的上下两表面接在电压恒为U的电源上.则( )
 电磁泵在目前的生产科技中得到了广泛应用.如图所示是电磁泵的原理图,泵体是一个长方体,ab边长为L,两侧端面是边长为a的正方形;流经泵体内的液体密度为ρ,在进口处接入电导率为σ(电阻率的倒数)的导电液,泵体所在处有方向垂直侧面向外的磁场B,泵体的上下两表面接在电压恒为U的电源上.则( )
电磁泵在目前的生产科技中得到了广泛应用.如图所示是电磁泵的原理图,泵体是一个长方体,ab边长为L,两侧端面是边长为a的正方形;流经泵体内的液体密度为ρ,在进口处接入电导率为σ(电阻率的倒数)的导电液,泵体所在处有方向垂直侧面向外的磁场B,泵体的上下两表面接在电压恒为U的电源上.则( )| A. | 泵体上表面应接电源正极 | |
| B. | 通过泵体的电流I=$\frac{UL}{σ}$ | |
| C. | 增大磁感应强度,每秒被抽液体的质量就越大 | |
| D. | 增大电导率σ,电磁驱动力所产生的附加压强越小 |
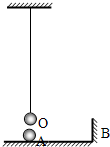 如图所示,有一摆长为L的单摆,当摆球经平衡位置O向右运动的瞬间,一个以速度v匀速运动的小球同时经过O点正下方的A点向右运动,并与竖直墙B碰撞后又以原速率返回,若不计球与墙碰撞的时间,求:B、A间的距离x满足什么条件时,才能使球返回时恰好与摆球同时分别经过A点与O点?
如图所示,有一摆长为L的单摆,当摆球经平衡位置O向右运动的瞬间,一个以速度v匀速运动的小球同时经过O点正下方的A点向右运动,并与竖直墙B碰撞后又以原速率返回,若不计球与墙碰撞的时间,求:B、A间的距离x满足什么条件时,才能使球返回时恰好与摆球同时分别经过A点与O点? 多用电表表头的示意图如图.
多用电表表头的示意图如图.