题目内容
17.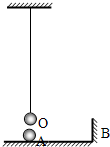 如图所示,有一摆长为L的单摆,当摆球经平衡位置O向右运动的瞬间,一个以速度v匀速运动的小球同时经过O点正下方的A点向右运动,并与竖直墙B碰撞后又以原速率返回,若不计球与墙碰撞的时间,求:B、A间的距离x满足什么条件时,才能使球返回时恰好与摆球同时分别经过A点与O点?
如图所示,有一摆长为L的单摆,当摆球经平衡位置O向右运动的瞬间,一个以速度v匀速运动的小球同时经过O点正下方的A点向右运动,并与竖直墙B碰撞后又以原速率返回,若不计球与墙碰撞的时间,求:B、A间的距离x满足什么条件时,才能使球返回时恰好与摆球同时分别经过A点与O点?
分析 单摆由静止释放后做简谐运动,经过半个周期的整数倍的时间时,两球再次相遇,求出B球运动的时间,再求解x.
解答 解:摆球A做简谐运动,当其与B球发生碰撞后速度改变,但是摆动的周期不变.
而B球做匀速直线运动,再次相遇的条件为B球来回所需要的时间为单摆半周期的整数倍.
B球运动时间t=n•$\frac{T}{2}$(n=1,2,3…)
又t=$\frac{2x}{v}$,T=$2π\sqrt{\frac{L}{g}}$
联立解得:x=$\frac{πnv}{2}\sqrt{\frac{L}{g}}$(n=1,2,3…)
答:B、A间距x满足x=$\frac{πnv}{2}\sqrt{\frac{L}{g}}$(n=1,2,3…),才能使球返回时恰好与摆球同时分别经过A点与O点.
点评 本题关键利用单摆的周期性和两球运动的同时性,不能当作特殊值求解,而认为B球运动的时间为单摆半个周期.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
5.如图所示的两种电路中,电源相同,电源内阻不计,各电阻器阻值相等,各电流表的内阻相等且不可忽略不计.电流表A1、A2、A3和A4读出的电流值分别为I1、I2、I3和I4.下列关系式中正确的是( )
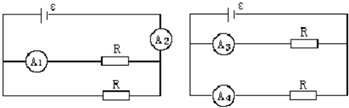

| A. | I1=I3 | B. | I1>I4 | C. | I2=2I1 | D. | I2<I3+I4 |
9.下列说法正确的是( )
| A. | 物体从外界吸收热量,其内能一定增加 | |
| B. | 热机的效率可以达到100% | |
| C. | 布朗运动是悬浮颗粒分子的无规则运动 | |
| D. | 叶面上的小露珠呈球形是由于液体表面张力的作用 |
7.如图所示,某大剧院的屋顶为半球形,一只小猴在该屋顶向上缓慢爬行,它在向上爬的过程中( )
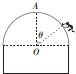

| A. | 屋顶对它的支持力变大 | B. | 屋顶对它的支持力变小 | ||
| C. | 屋顶对它的摩擦力变大 | D. | 屋顶对它的作用力变小 |
 如图所示,有一质量为0.5kg的小球,用绳子系住小球在竖直平面内做圆周运动,转动半径为0.5m,小球通过最高点的速度为4m/s,不计空气阻力,g取10m/s2,
如图所示,有一质量为0.5kg的小球,用绳子系住小球在竖直平面内做圆周运动,转动半径为0.5m,小球通过最高点的速度为4m/s,不计空气阻力,g取10m/s2, 为了较准确地测量某细线能承受的最大拉力,小聪、小明分别进行了如下实验:
为了较准确地测量某细线能承受的最大拉力,小聪、小明分别进行了如下实验: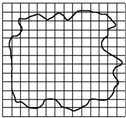 油酸酒精溶液的浓度为每10 000mL油酸酒精溶液中有油酸6mL,用滴管向量筒内滴75滴上述溶液,量筒中的溶液体积增加1mL.若把一滴这样的溶液入盛水的浅盘中,由于酒精溶于水,油酸在水面展开,稳定后形成的单分子油膜的形状如图所示.
油酸酒精溶液的浓度为每10 000mL油酸酒精溶液中有油酸6mL,用滴管向量筒内滴75滴上述溶液,量筒中的溶液体积增加1mL.若把一滴这样的溶液入盛水的浅盘中,由于酒精溶于水,油酸在水面展开,稳定后形成的单分子油膜的形状如图所示.