Question

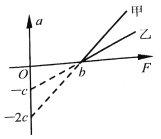
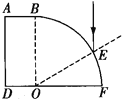
【题目】图示为用透明介质做成的一块棱镜的截面图，其中是矩形，是半径为的四分之一圆，圆心为。一条光线从面上的E点垂直于入射，它进入棱镜后恰好在面上的点(图中未画出)发生全反射后经过点，已知棱镜对该光的折射率为，光在真空中的传播速度为求：(结果可用根号表示)

(i)的正切值；

(ii)光线从点传播到点所需的时间。

Answer 1

【答案】（1）+1；（2）

【解析】

（1）光在M点恰好发生全反射然后经过A点，根据求解临界角，根据光的折射定律结合几何关系求解∠BOE的正切值；（2）根据几何关系求解光在棱镜中的传播距离，根据v=c/n求解速度，根据t=x/v求解时间.

（1）光线入射到BE面上的E点时，入射角为i，折射角为θ，光在M点恰好发生全反射，入射角为C，则

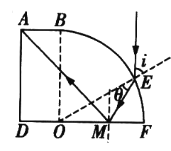
由几何关系可知：∠BOE=i，；，则；由折射定律：

即

解得tani=+1

故∠BOE的正切值为+1；

（2）

在AMD中：

光在该棱镜中的传播速度：

故所求的时间：