题目内容
如图,水平地面上有一转台,高h=10米,由半径为R=1米和r=0.5米的两个半圆柱拼合而成,可绕其中心轴转动,平台边缘上放有两个质量均为m=0.1kg的物体,可视为质点,由一根长为1.5m的细线连接在一起,且细线过转台的圆心,A、B两物体与平台接触面的动摩擦系数均为μ=0.2,最大静摩擦力等于滑动摩擦力.现在使转台转动的角速度缓慢地增大,g=10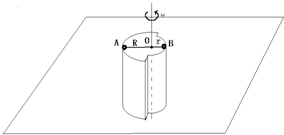 m/s2,求:
m/s2,求:
(1)在绳子无张力时,ω的最大值为多少?
(2)在A、B两个物体不滑动时,ω的最大值又为多少?
(3)接第2小题,当ω取最大值时,绳子突然断裂,A、B两个物体将同时离开转台,当两个物体同时第一次着地时,其着地点距离是多少?(结果带上根号)
 m/s2,求:
m/s2,求:(1)在绳子无张力时,ω的最大值为多少?
(2)在A、B两个物体不滑动时,ω的最大值又为多少?
(3)接第2小题,当ω取最大值时,绳子突然断裂,A、B两个物体将同时离开转台,当两个物体同时第一次着地时,其着地点距离是多少?(结果带上根号)
分析:(1)在绳子无张力时,AB两个物体靠静摩擦力提供向心力,当一个物体达到最大静摩擦力时,绳子开始有张力,根据向心力公式即可求解此时的角速度;
(2)当A、B两个物体刚好不滑动时,对两个物体进行受力分析,根据合外力提供向心力列式即可求解;
(3)绳子突然断裂时,A、B两个物体将做平抛运动,根据v=ωr求出AB的线速度,再根据平抛运动的基本公式即可求解.
(2)当A、B两个物体刚好不滑动时,对两个物体进行受力分析,根据合外力提供向心力列式即可求解;
(3)绳子突然断裂时,A、B两个物体将做平抛运动,根据v=ωr求出AB的线速度,再根据平抛运动的基本公式即可求解.
解答:解:(1)在绳子无张力时,AB两个物体靠静摩擦力提供向心力,根据f=mω2r可知,A的半径大,所以A最先达到最大静摩擦力,则有:
μmg=mω2R
解得:ω=
=
=
rad/s
(2)当A、B两个物体刚好不滑动时,两物体都达到最大静摩擦力,设此时绳子的拉力为T,则
T+μmg=mω′2R…①
T-μmg=mω′2r…②
由①-②解得:
ω′=2
rad/s
(3)绳子突然断裂时,A、B两个物体将做平抛运动,
此时A的速度vA=ω′R=2
×1=2
m/s
B的速度vA=ω′r=2
×0.5=
m/s
平抛运动的时间t=
=
=
s
则A物体水平距离为xA=vAt=2
?
=4m
A物体水平距离为xB=vBt=
?
=2m
根据几何关系得:着地点距离x=
=
=
m
答:(1)在绳子无张力时,ω的最大值为
rad/s;
(2)在A、B两个物体不滑动时,ω的最大值又为2
rad/s;
(3)接第2小题,当ω取最大值时,绳子突然断裂,A、B两个物体将同时离开转台,当两个物体同时第一次着地时,其着地点距离为
m.
μmg=mω2R
解得:ω=
|
|
| 2 |
(2)当A、B两个物体刚好不滑动时,两物体都达到最大静摩擦力,设此时绳子的拉力为T,则
T+μmg=mω′2R…①
T-μmg=mω′2r…②
由①-②解得:
ω′=2
| 2 |
(3)绳子突然断裂时,A、B两个物体将做平抛运动,
此时A的速度vA=ω′R=2
| 2 |
| 2 |
B的速度vA=ω′r=2
| 2 |
| 2 |
平抛运动的时间t=
|
|
| 2 |
则A物体水平距离为xA=vAt=2
| 2 |
| 2 |
A物体水平距离为xB=vBt=
| 2 |
| 2 |
根据几何关系得:着地点距离x=
| (xA+xB)2+(R+r)2 |
| 62+1.52 |
| 38.25 |
答:(1)在绳子无张力时,ω的最大值为
| 2 |
(2)在A、B两个物体不滑动时,ω的最大值又为2
| 2 |
(3)接第2小题,当ω取最大值时,绳子突然断裂,A、B两个物体将同时离开转台,当两个物体同时第一次着地时,其着地点距离为
| 38.25 |
点评:本题的关键是抓住临界状态,隔离物体,对物体进行正确受力分析,根据向心力公式求解,第三问中要注意着地点的距离不是两物体做平抛运动的水平位移之和,难度适中.

练习册系列答案
相关题目
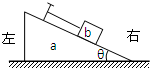 如图,水平地面上有一楔形物块a,其斜面上有一小物块b,b与平行于斜面的细绳的一端相连,细绳的另一端固定在斜面上.a与b之间光滑,a和b以共同速度在地面轨道的光滑段向左运动.当它们刚运行至轨道的粗糙段时,关于b之后的运动情况和地面对a的支持力,下列说法中正确的是( )
如图,水平地面上有一楔形物块a,其斜面上有一小物块b,b与平行于斜面的细绳的一端相连,细绳的另一端固定在斜面上.a与b之间光滑,a和b以共同速度在地面轨道的光滑段向左运动.当它们刚运行至轨道的粗糙段时,关于b之后的运动情况和地面对a的支持力,下列说法中正确的是( )| A、b将一定沿a的斜面上滑,地面对a的支持力减小 | B、b可能相对a的斜面静止,地面对a的支持力不变 | C、b将一定沿a的斜面上滑,地面对a的支持力增大 | D、绳的张力一定减小,b一定相对a的斜面静止,地面对a的支持力不变 |
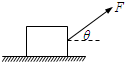 如图,水平地面上有一木箱,木箱与地面间的动摩擦因数为μ,木箱在与水平夹角为θ的拉力F作用下做匀速直线运动.在θ从0逐渐增大到90°的过程中,木箱的速度始终保持不变,则拉力F的功率( )
如图,水平地面上有一木箱,木箱与地面间的动摩擦因数为μ,木箱在与水平夹角为θ的拉力F作用下做匀速直线运动.在θ从0逐渐增大到90°的过程中,木箱的速度始终保持不变,则拉力F的功率( )| A、一直增大 | B、一直减小 | C、先减小后增大 | D、先增大后减小 |
 (2008?海南)如图,水平地面上有一楔形物体b,b的斜面上有一小物块a;a与b之间、b与地面之间均存在摩擦.已知楔形物体b静止时,a静止在b的斜面上.现给a和b一个共同的向左的初速度,与a和b都静止时相比,此时可能( )
(2008?海南)如图,水平地面上有一楔形物体b,b的斜面上有一小物块a;a与b之间、b与地面之间均存在摩擦.已知楔形物体b静止时,a静止在b的斜面上.现给a和b一个共同的向左的初速度,与a和b都静止时相比,此时可能( )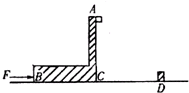 如图,水平地面上有一“L”型滑板ACB,A到地面的竖直高度为h=1.8m.水
如图,水平地面上有一“L”型滑板ACB,A到地面的竖直高度为h=1.8m.水