题目内容
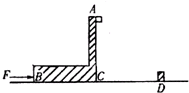 如图,水平地面上有一“L”型滑板ACB,A到地面的竖直高度为h=1.8m.水
如图,水平地面上有一“L”型滑板ACB,A到地面的竖直高度为h=1.8m.水平地面上D处有一固定障碍物,滑板右端C到障碍物的距离为x=1.28m滑板左端加上水平向右的推力F同时,有一小物块紧贴竖直板的A点无初速释放,小物块恰好能在滑板上与滑板一起保持相对静止.滑板撞到障碍物时立即撤去力F,滑板以原速率反弹.小物块最终落在地面上.滑板质量M=3kg,物块质量m=lkg,滑板与物块及地面间的动摩擦因数均为0.4(取g=m/s2,sin37°=0.6).求:
(1)滑板撞到障碍物前受到的水平推力F;
(2)物块落地时速度的大小和方向;
(3)物块落地时到滑板C端的距离.
分析:(1)对整体运用牛顿第二定律,求出滑板撞到障碍物前的水平推力.
(2)滑板碰到障碍物后,物块做平抛运动,平抛运动的初速度等于滑板撞到障碍物时的速度,根据平抛运动的规律求出物块落地时的速度大小和方向.
(3)碰到障碍物后,物块做平抛运动,木板反弹做匀减速直线运动,求出平抛运动的水平位移,以及在平抛运动过程中木板反弹的位移,两者位移之和为物块落地时到滑板C端的距离.
(2)滑板碰到障碍物后,物块做平抛运动,平抛运动的初速度等于滑板撞到障碍物时的速度,根据平抛运动的规律求出物块落地时的速度大小和方向.
(3)碰到障碍物后,物块做平抛运动,木板反弹做匀减速直线运动,求出平抛运动的水平位移,以及在平抛运动过程中木板反弹的位移,两者位移之和为物块落地时到滑板C端的距离.
解答:解:(1)对m有:
N=ma
μN=mg
解得:a=
═
m/s2=25m/s2
物体与滑板相对静止,向右的加速度为a,
则F-μ(m+M)g=(M+m)a
解得:F=μ(m+M)g+(M+m)a=0.4×(1+3)×10+(1+3)×25=116N
(2)设滑板撞到障碍物时的速度大小为v1,
v12=2ax
解得:
v1=
=
m/s=8m/s
撞到障碍物后物块做平抛运动,
h=
gt2
解得:
t=
=
=0.6s
又:vy=gt
解得:
vy=
=
m/s=6m/s
落地速度为:
v=
=
m/s=10m/s.
速度与水平方向的夹角为α
tanα=
=
=
,则α=37°.
(3)物块的水平位移x1=v1t=4.8m
滑板运动的加速度为a2,μMg=Ma2
解得:
a2=μg=0.4×10m/s2=4m/s2
滑板停止运动时间:
t1=
=
s=2s
则物块落地时,板尚未停止运动.
滑板向右运动的距离:
x2=v1t-
a2t2=8×0.6-
×4×0.62=4.08m
物块落地时到B的距离为x=x1+x2=8.88m.
答:(1)滑板撞到障碍物前物块受到的力为116N.(2)物块落地时的速度大小为10m/s,方向与水平方向成37度角.(3)物块落地时到滑板B端的距离为8.88m.
N=ma
μN=mg
解得:a=
| g |
| μ |
| 10 |
| 0.4 |
物体与滑板相对静止,向右的加速度为a,
则F-μ(m+M)g=(M+m)a
解得:F=μ(m+M)g+(M+m)a=0.4×(1+3)×10+(1+3)×25=116N
(2)设滑板撞到障碍物时的速度大小为v1,
v12=2ax
解得:
v1=
| 2ax |
| 2×25×1.28 |
撞到障碍物后物块做平抛运动,
h=
| 1 |
| 2 |
解得:
t=
|
|
又:vy=gt
解得:
vy=
| 2gh |
| 2×10×1.8 |
落地速度为:
v=
| v12+vy2 |
| 82+62 |
速度与水平方向的夹角为α
tanα=
| vy |
| v1 |
| 6 |
| 8 |
| 3 |
| 4 |
(3)物块的水平位移x1=v1t=4.8m
滑板运动的加速度为a2,μMg=Ma2
解得:
a2=μg=0.4×10m/s2=4m/s2
滑板停止运动时间:
t1=
| v1 |
| a2 |
| 8 |
| 4 |
则物块落地时,板尚未停止运动.
滑板向右运动的距离:
x2=v1t-
| 1 |
| 2 |
| 1 |
| 2 |
物块落地时到B的距离为x=x1+x2=8.88m.
答:(1)滑板撞到障碍物前物块受到的力为116N.(2)物块落地时的速度大小为10m/s,方向与水平方向成37度角.(3)物块落地时到滑板B端的距离为8.88m.
点评:解决本题的关键能够正确地受力分析,确定物体的运动情况,结合牛顿第二定律和运动学公式进行求解.

练习册系列答案
相关题目
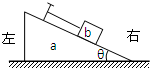 如图,水平地面上有一楔形物块a,其斜面上有一小物块b,b与平行于斜面的细绳的一端相连,细绳的另一端固定在斜面上.a与b之间光滑,a和b以共同速度在地面轨道的光滑段向左运动.当它们刚运行至轨道的粗糙段时,关于b之后的运动情况和地面对a的支持力,下列说法中正确的是( )
如图,水平地面上有一楔形物块a,其斜面上有一小物块b,b与平行于斜面的细绳的一端相连,细绳的另一端固定在斜面上.a与b之间光滑,a和b以共同速度在地面轨道的光滑段向左运动.当它们刚运行至轨道的粗糙段时,关于b之后的运动情况和地面对a的支持力,下列说法中正确的是( )| A、b将一定沿a的斜面上滑,地面对a的支持力减小 | B、b可能相对a的斜面静止,地面对a的支持力不变 | C、b将一定沿a的斜面上滑,地面对a的支持力增大 | D、绳的张力一定减小,b一定相对a的斜面静止,地面对a的支持力不变 |
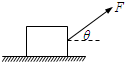 如图,水平地面上有一木箱,木箱与地面间的动摩擦因数为μ,木箱在与水平夹角为θ的拉力F作用下做匀速直线运动.在θ从0逐渐增大到90°的过程中,木箱的速度始终保持不变,则拉力F的功率( )
如图,水平地面上有一木箱,木箱与地面间的动摩擦因数为μ,木箱在与水平夹角为θ的拉力F作用下做匀速直线运动.在θ从0逐渐增大到90°的过程中,木箱的速度始终保持不变,则拉力F的功率( )| A、一直增大 | B、一直减小 | C、先减小后增大 | D、先增大后减小 |
 (2008?海南)如图,水平地面上有一楔形物体b,b的斜面上有一小物块a;a与b之间、b与地面之间均存在摩擦.已知楔形物体b静止时,a静止在b的斜面上.现给a和b一个共同的向左的初速度,与a和b都静止时相比,此时可能( )
(2008?海南)如图,水平地面上有一楔形物体b,b的斜面上有一小物块a;a与b之间、b与地面之间均存在摩擦.已知楔形物体b静止时,a静止在b的斜面上.现给a和b一个共同的向左的初速度,与a和b都静止时相比,此时可能( )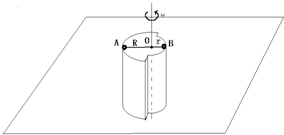 m/s2,求:
m/s2,求: