题目内容
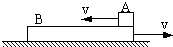如图所示，一质量M=3kg的长方形木板序放在光滑水平地面上，在其右端放一质量m=l kg的小术块A现以地面为参照系，给A和B以大小均为4.0m/s，方向相反的初速度，使A开始向左运动，B开始向右运动，但最后月并没有滑离B板，站在地面的观察者看到在一段时间内小木块A正在做加速运动，则在这段时间内的某时刻木板B相对地面的速度大小可能是（ ）分析：对木板与木块组成的系统，合外力保持为零，系统的总动量守恒．A先向左减速，到速度减小零后向右加速到速度与B相同，此过程A正在做加速运动，根据动量守恒定律求出A的速度为零时B的速度，以及两者相对静止时共同速度，确定出A正在做加速运动时，B的速度范围，再进行选择．
解答：解：取水平向右方向为正方向．当A的速度为零，根据动量守恒定律得：
（M-m）v0=MvB1，解得，此时B的速度为vB1=2.67m/s
当AB速度相同时，则有
（M-m）v0=（M+m）vB2，解得，vB2=2m/s
则在木块A正在做加速运动的时间内B的速度范围为2m/s＜vB＜2.67m/s．
故选A
（M-m）v0=MvB1，解得，此时B的速度为vB1=2.67m/s
当AB速度相同时，则有
（M-m）v0=（M+m）vB2，解得，vB2=2m/s
则在木块A正在做加速运动的时间内B的速度范围为2m/s＜vB＜2.67m/s．
故选A
点评：本题运用动量守恒定律求解B的速度范围，由于不考虑过程的细节，比牛顿第二定律要简捷．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，一质量M=50kg、长L=3m的平板车静止在光滑的水平地面上，平板车上表面距地面的高度h=1.8m．一质量m=10kg可视为质点的滑块，以v0=7.5m/s的初速度从左端滑上平板车，滑块与平板车间的动摩擦因数μ=0.5，取g=10m/s2．
如图所示，一质量M=3.0kg的长方形木板B放在光滑水平地面上，在其右端放一质量m=1.0kg的小木块A，现以地面为参照系，给A和B以大小均为4.0m/s，方向相反的初速度，使A开始向左运动，B开始向右运动，最后A相对B静止，此时A的速度为（ ）
如图所示，一质量M=2kg的斜面体静止在水平地面上，斜面体与地面间的动摩擦因数为μ=0.5，斜面夹角α=37°．一质量m=1kg的光滑小球放在斜面体与竖直墙壁之间，处于静止状态．若在光滑小球的正上方施加一个竖直向下的力，要使斜面体向右移动，竖直向下的力F至少为多大？（设滑动摩擦力等于最大静摩擦力，g取10m/s2）
（2011?太原模拟）如图所示，一质量m=65kg的选手参加“挑战极限运动”，要在越过宽度s=3m的水沟后跃上高h=1.8m的平台．他采用的方法是：手握长L=3.05m的轻质弹性杆一端，从A点由静止开始匀加速助跑，至B点时，杆另一端抵在O点的阻挡物上，接着杆发生形变，同时人蹬地后被弹起，到达最高点时杆处于竖直（不弯曲），人的重心恰好位于杆的顶端，此刻人放开杆水平飞出，最终落到平台上（重心恰在平台表面）．不计运动过程中的空气阻力，取g=10m/s2：