题目内容
如图所示，宽度为d1的I区里有与水平方向成45°角的匀强电场E1，宽度为d2的II区里有相互正交的匀强磁场B和匀强电场E2．一带电量为q，质量为m的微粒自图中I区左边界线上的P点由静止释放后水平向右做直线运动进入II区的复合场再做匀速圆周运动到右边界上的Q点，其速度方向改变了60°，重力加速度为g．（d1、E1、E2未知）求：（1）E1、E2的大小；
（2）有界电场E1的宽度d1．
分析：（1）根据各自受力分析，结合受力平衡状态方程，及力的平行四边形定则，即可求解；
（2）根据洛伦兹力提供向心力，结合牛顿第二定律与几何关系，即可求解．
（2）根据洛伦兹力提供向心力，结合牛顿第二定律与几何关系，即可求解．
解答：解：（1）由题意有：qE1sin45°=mg
qE2=mg
∴E1=
E2=
（2）设微粒在复合场中做匀速圆周运动的速率为v，轨道半径为R，由几何关系有：
Rsin60°=d2
由qvB=m
有：R=
联立求得：
v=
=
微粒在I区中加速时有：
qE1cos45°×d1=
mv2
或由v2=2ad1而a=
解得：d1=
答：（1）两电场强度的大小分别为E1=
，E2=
；
（2）有界电场E1的宽度d1=
．
qE2=mg
∴E1=
| ||
| q |
E2=
| mg |
| q |
（2）设微粒在复合场中做匀速圆周运动的速率为v，轨道半径为R，由几何关系有：
Rsin60°=d2
由qvB=m
| v2 |
| R |
| mv |
| qB |
联立求得：
v=
| qBd2 |
| msin60° |
2
| ||
| 3m |
微粒在I区中加速时有：
qE1cos45°×d1=
| 1 |
| 2 |
或由v2=2ad1而a=
| qE1cos45° |
| m |
解得：d1=
2q2B2
| ||
| 3m2g |
答：（1）两电场强度的大小分别为E1=
| ||
| q |
| mg |
| q |
（2）有界电场E1的宽度d1=
2q2B2
| ||
| 3m2g |
点评：考查受力分析的方法，掌握受力平衡状态方程，理解力的平行四边形定则与牛顿第二定律的应用，注意几何关系在本题的运用．
练习册系列答案
相关题目
（2012?无锡二模）如图所示，间距为L的两条足够长的平行绝缘轨道与水平面的夹角为θ，两轨道间有n个长方形匀强磁场区域，磁场区域的宽度为d1，区域与区域之间的距离为d2，匀强磁场的磁感应强度为B、方向与导轨平面垂直．一长L′（略大于L）、宽为l、质量为m、电阻为R的长方形导体线圈放在导轨上，线圈恰能保持静止．现给线圈一个沿轨道平面向下的初速度，线圈恰好滑过n个磁场区域后停止，线圈在运动过程中的长边始终与轨道垂直．空气阻力和线圈导线的粗细不计，重力加速度为g，最大静摩擦力等于滑动摩擦力，d1=d2=l．求：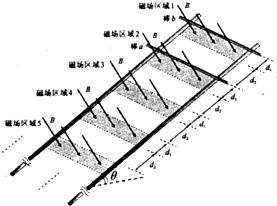
如图所示，间距为L的两条足够长的平行金属导轨与水平面的夹角为θ，导轨光滑且电阻忽略不计．场强为B的条形匀强磁场方向与导轨平面垂直，磁场区域的宽度为d1，间距为d2．两根质量均为m、有效电阻均为R的导体棒a和b放在导轨上，并与导轨垂直． （设重力加速度为g） 
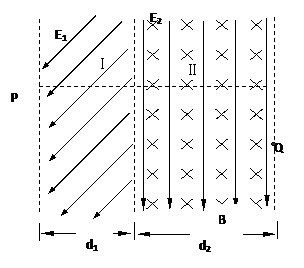如图所示，宽度为d1的I区里有与水平方向成45°角的匀强电场E1，宽度为d2的II区里有相互正交的匀强磁场B和匀强电场E2。一