题目内容
15.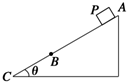 如图所示,固定斜面倾角为θ,整个斜面长分为AB、BC两段,AB=2BC.小物块P(可视为质点)与AB、BC两段斜面间的动摩擦因数分别为μ1、μ2.已知P由静止开始从A点释放,恰好能滑动到C点而停下,则,下列说法正确的是( )
如图所示,固定斜面倾角为θ,整个斜面长分为AB、BC两段,AB=2BC.小物块P(可视为质点)与AB、BC两段斜面间的动摩擦因数分别为μ1、μ2.已知P由静止开始从A点释放,恰好能滑动到C点而停下,则,下列说法正确的是( )| A. | μ1>tanθ | B. | μ2<tanθ | C. | tanθ=2μ1-μ2 | D. | tanθ=$\frac{{2{μ_1}+{μ_2}}}{3}$ |
分析 对物块进行受力分析,分析下滑过程中哪些力做功.运用动能定理研究A点释放,恰好能滑动到C点而停下,列出等式找出答案.
解答 解:A点释放,恰好能滑动到C点,物块受重力、支持力、滑动摩擦力.
设斜面AC长为L,运用动能定理研究A点释放,恰好能滑动到C点而停下,列出等式:
mgLsinθ-μ1mgcosθ×$\frac{1}{3}L$-μ2mgcosθ×$\frac{2}{3}L$=0-0=0
解得:tanθ=$\frac{2{μ}_{1}+{μ}_{2}}{3}$.故C错误,D正确.
在AB段,物体做加速运动,则有:mgsinθ>μ1mgcosθ,解得μ1<tanθ,在BC段做减速运动,则有:mgsinθ<μ2mgcosθ,解得μ2>tanθ,故A、B错误.
故选:D.
点评 了解研究对象的运动过程是解决问题的前提,根据题目已知条件和求解的物理量选择物理规律解决问题.要注意运动过程中力的变化.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.对光学现象的认识,以下说法中正确的是( )
| A. | 立体电影利用了光的偏振原理 | |
| B. | 光学镜头上的增透膜是利用光的全反射现象 | |
| C. | 光纤通信利用了光的衍射现象 | |
| D. | 海市蜃楼和彩虹一样都是仅由光的折射形成的 |
6.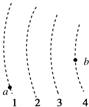 如图所示,虚线所示为静电场中的等势面1、2、3、4,相邻的等势面之间的电势差相等,其中等势面2的电势为0.一带正电的点电荷在静电力的作用下运动,经过a、b点时的动能分别为26eV和5eV.当这一点电荷运动到某一位置,其电势能变为-8eV,它的动能应为( )
如图所示,虚线所示为静电场中的等势面1、2、3、4,相邻的等势面之间的电势差相等,其中等势面2的电势为0.一带正电的点电荷在静电力的作用下运动,经过a、b点时的动能分别为26eV和5eV.当这一点电荷运动到某一位置,其电势能变为-8eV,它的动能应为( )
 如图所示,虚线所示为静电场中的等势面1、2、3、4,相邻的等势面之间的电势差相等,其中等势面2的电势为0.一带正电的点电荷在静电力的作用下运动,经过a、b点时的动能分别为26eV和5eV.当这一点电荷运动到某一位置,其电势能变为-8eV,它的动能应为( )
如图所示,虚线所示为静电场中的等势面1、2、3、4,相邻的等势面之间的电势差相等,其中等势面2的电势为0.一带正电的点电荷在静电力的作用下运动,经过a、b点时的动能分别为26eV和5eV.当这一点电荷运动到某一位置,其电势能变为-8eV,它的动能应为( )| A. | 6 eV | B. | 13 eV | C. | 20 eV | D. | 27 eV |
3.当波从一中介质进入另一种介质时,保持不变的物理量是( )
| A. | 波长 | B. | 波速 | C. | 频率 | D. | 周期 |
10.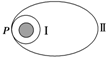 “嫦娥”一号在奔月的过程中,要进行多次轨道调控.假设要使其从圆轨道Ⅰ转移到椭圆轨道Ⅱ(P为两轨道的切点),则下列说法正确的是( )
“嫦娥”一号在奔月的过程中,要进行多次轨道调控.假设要使其从圆轨道Ⅰ转移到椭圆轨道Ⅱ(P为两轨道的切点),则下列说法正确的是( )
 “嫦娥”一号在奔月的过程中,要进行多次轨道调控.假设要使其从圆轨道Ⅰ转移到椭圆轨道Ⅱ(P为两轨道的切点),则下列说法正确的是( )
“嫦娥”一号在奔月的过程中,要进行多次轨道调控.假设要使其从圆轨道Ⅰ转移到椭圆轨道Ⅱ(P为两轨道的切点),则下列说法正确的是( )| A. | “嫦娥”一号应在P点启动火箭向后喷气 | |
| B. | “嫦娥”一号应在P点启动火箭向前喷气 | |
| C. | “嫦娥”一号在椭圆轨道上运动时,机械能不守恒 | |
| D. | “嫦娥”一号在椭圆轨道上运动的周期与在圆轨道上运动的周期相同 |
20. 如图所示,在竖直平面内有一半径为R的圆弧轨道,半径OA水平、OB竖直,一个质量为m的小球(视为质点)自A的正上方P点由静止开始自由下落,小球沿轨道到达最高点B时恰好对轨道没有压力.已知AP=2R,重力加速度为g,则小球从P到B的运动过程中( )
如图所示,在竖直平面内有一半径为R的圆弧轨道,半径OA水平、OB竖直,一个质量为m的小球(视为质点)自A的正上方P点由静止开始自由下落,小球沿轨道到达最高点B时恰好对轨道没有压力.已知AP=2R,重力加速度为g,则小球从P到B的运动过程中( )
 如图所示,在竖直平面内有一半径为R的圆弧轨道,半径OA水平、OB竖直,一个质量为m的小球(视为质点)自A的正上方P点由静止开始自由下落,小球沿轨道到达最高点B时恰好对轨道没有压力.已知AP=2R,重力加速度为g,则小球从P到B的运动过程中( )
如图所示,在竖直平面内有一半径为R的圆弧轨道,半径OA水平、OB竖直,一个质量为m的小球(视为质点)自A的正上方P点由静止开始自由下落,小球沿轨道到达最高点B时恰好对轨道没有压力.已知AP=2R,重力加速度为g,则小球从P到B的运动过程中( )| A. | 重力做功2mgR | B. | 机械能减少mgR | ||
| C. | 合力做功mgR | D. | 克服摩擦力做功$\frac{1}{2}$mgR |
7.足球运动员将一只沿水平方向飞来的足球反向踢回的过程中,若足球动量变化量的大小为10kg•m/s,则( )
| A. | 足球的动量一定减小 | B. | 足球的动量一定增大 | ||
| C. | 足球的动量大小可能不变 | D. | 足球的动量大小一定变化 |
10. 在一水平向右匀速运动的传送带的左端A点,每隔时间T轻放上一个相同的工件,已知工件与传送带间动摩擦因数为μ,工件质量均为m,经测量,发现那些已经和传送带达到相同速度的工件之间的距离为x.下列判断一定正确的是( )
在一水平向右匀速运动的传送带的左端A点,每隔时间T轻放上一个相同的工件,已知工件与传送带间动摩擦因数为μ,工件质量均为m,经测量,发现那些已经和传送带达到相同速度的工件之间的距离为x.下列判断一定正确的是( )
 在一水平向右匀速运动的传送带的左端A点,每隔时间T轻放上一个相同的工件,已知工件与传送带间动摩擦因数为μ,工件质量均为m,经测量,发现那些已经和传送带达到相同速度的工件之间的距离为x.下列判断一定正确的是( )
在一水平向右匀速运动的传送带的左端A点,每隔时间T轻放上一个相同的工件,已知工件与传送带间动摩擦因数为μ,工件质量均为m,经测量,发现那些已经和传送带达到相同速度的工件之间的距离为x.下列判断一定正确的是( )| A. | 传送带的速度为$\frac{x}{T}$ | |
| B. | 传送带的速度为2$\sqrt{2μgx}$ | |
| C. | 每个工件与传送带间因摩擦而产生的热量为$\frac{1}{2}$μmgx | |
| D. | 在一段相当长的时间t内,传送带因为传送工作而多消耗的能量为$\frac{mt{x}^{2}}{{T}^{2}}$ |
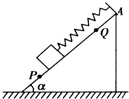 如图所示,在倾角α=60°的斜面上,放一质量为10kg的物体,用k=100N/m的轻质弹簧平行于斜面拉着,物体放在PQ之间任何位置都能处于静止状态,而超过这一范围,物体就会沿斜面滑动,若AP=22cm,AQ=8cm,试求物体与斜面间的最大静摩擦力的大小?(sin60°=$\frac{\sqrt{3}}{2}$,cos60°=$\frac{1}{2}$)
如图所示,在倾角α=60°的斜面上,放一质量为10kg的物体,用k=100N/m的轻质弹簧平行于斜面拉着,物体放在PQ之间任何位置都能处于静止状态,而超过这一范围,物体就会沿斜面滑动,若AP=22cm,AQ=8cm,试求物体与斜面间的最大静摩擦力的大小?(sin60°=$\frac{\sqrt{3}}{2}$,cos60°=$\frac{1}{2}$)