��Ŀ����
10��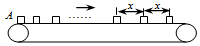 ��һˮƽ���������˶��Ĵ��ʹ������A�㣬ÿ��ʱ��T�����һ����ͬ�Ĺ�������֪�����봫�ʹ��䶯Ħ������Ϊ�̣�����������Ϊm����������������Щ�Ѿ��ʹ��ʹ��ﵽ��ͬ�ٶȵĹ���֮��ľ���Ϊx�������ж�һ����ȷ���ǣ�������
��һˮƽ���������˶��Ĵ��ʹ������A�㣬ÿ��ʱ��T�����һ����ͬ�Ĺ�������֪�����봫�ʹ��䶯Ħ������Ϊ�̣�����������Ϊm����������������Щ�Ѿ��ʹ��ʹ��ﵽ��ͬ�ٶȵĹ���֮��ľ���Ϊx�������ж�һ����ȷ���ǣ�������| A�� | ���ʹ����ٶ�Ϊ$\frac{x}{T}$ | |
| B�� | ���ʹ����ٶ�Ϊ2$\sqrt{2��gx}$ | |
| C�� | ÿ�������봫�ʹ�����Ħ��������������Ϊ$\frac{1}{2}$��mgx | |
| D�� | ��һ���൱����ʱ��t�ڣ����ʹ���Ϊ�������������ĵ�����Ϊ$\frac{mt{x}^{2}}{{T}^{2}}$ |
���� �����ڴ��ʹ��������ȼ���ֱ���˶���Ȼ��������ֱ���˶���ÿ���������ϴ��ʹ����˶��Ĺ�����ͬ��ͨ��x=vT������ʹ����ٶȣ������ȼ��ٶ�֪ʶ����˶���ʱ�䣬���ݹ����ʹ��ʹ�֮������·�̴�С�����Ħ�����������������������غ�֪�������ĵ�����һ����ת��Ϊ�����Ķ��ܣ�һ����ת��ΪĦ�����������ܣ�
��� �⣺A�������ڴ��ʹ��������ȼ���ֱ���˶���Ȼ��������ֱ���˶���ÿ���������ϴ��ʹ����˶��Ĺ�����ͬ����֪x=vT����ô��ʹ����ٶ�v=$\frac{L}{T}$����A��ȷ��
B����ÿ�������ȼ����˶���ʱ��Ϊt������ţ�ٵڶ����ɵã������ļ��ٶ�Ϊ��g������v=v0+at����ã�t=$\frac{v}{a}=\frac{L}{T��g}$����B����
C�������봫�ʹ���Ի�����·��Ϊ��$��x=v\frac{v}{��g}-\frac{{v}^{2}}{2��g}=\frac{{v}^{2}}{2��g}=\frac{{L}^{2}}{2��g{T}^{2}}$����Ħ������������Ϊ��Q=$��mg��x=\frac{m{L}^{2}}{2{T}^{2}}$����C����
D�����������غ�ã����ʹ�����һ�����������ĵ�����E=$\frac{1}{2}$$m{v}^{2}+��mg��x=\frac{m{L}^{2}}{{T}^{2}}$����ʱ��t�ڣ��������ĸ���n=$\frac{t}{T}$��������ĵ�����$E��=nE=\frac{mt{L}^{2}}{{T}^{3}}$����D��ȷ��
��ѡ��AD��
���� �������Ĺؼ�֪�������ڴ��ʹ��ϵ��˶����ɣ�֪�����������ڴ��ʹ��ϵ��˶�������ͬ�����ţ�ٵڶ����ɡ��˶�ѧ��ʽ�������غ��ۺ���⣮

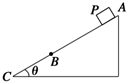 ��ͼ��ʾ���̶�б�����Ϊ�ȣ�����б�泤��ΪAB��BC���Σ�AB=2BC��С���P������Ϊ�ʵ㣩��AB��BC����б���Ķ�Ħ�������ֱ�Ϊ��1����2����֪P�ɾ�ֹ��ʼ��A���ͷţ�ǡ���ܻ�����C���ͣ�£�������˵����ȷ���ǣ�������
��ͼ��ʾ���̶�б�����Ϊ�ȣ�����б�泤��ΪAB��BC���Σ�AB=2BC��С���P������Ϊ�ʵ㣩��AB��BC����б���Ķ�Ħ�������ֱ�Ϊ��1����2����֪P�ɾ�ֹ��ʼ��A���ͷţ�ǡ���ܻ�����C���ͣ�£�������˵����ȷ���ǣ�������| A�� | ��1��tan�� | B�� | ��2��tan�� | C�� | tan��=2��1-��2 | D�� | tan��=$\frac{{2{��_1}+{��_2}}}{3}$ |
 �������ֳ�����һ�ֽС�Ħ���֡���������ʩ����ͼ��ʾ���������е��ο����ֵ�ת����������Բ���˶����Դ�������˵����������ȷ���ǣ�������
�������ֳ�����һ�ֽС�Ħ���֡���������ʩ����ͼ��ʾ���������е��ο����ֵ�ת����������Բ���˶����Դ�������˵����������ȷ���ǣ�������| A�� | �οʹ���һ��ƽ��״̬ | B�� | �ο�������һ�ֱ���������˶� | ||
| C�� | �ο�������һ���ȱ����˶� | D�� | �ο͵Ļ�е���غ� |
 һ�����������Բ�̴�����ֱ���ڣ������ƹ���Բ�ĵ�ˮƽ�������ת��������ת��ʱ�����������ˮƽ���ϵ�С���뾲ֹʱ��ָ����ͼ��ʾ���������ҿ�������Բ����ʱ�������תʱ��С����N��ָ������
һ�����������Բ�̴�����ֱ���ڣ������ƹ���Բ�ĵ�ˮƽ�������ת��������ת��ʱ�����������ˮƽ���ϵ�С���뾲ֹʱ��ָ����ͼ��ʾ���������ҿ�������Բ����ʱ�������תʱ��С����N��ָ������| A�� | ��ƫת | B�� | ��ֽ��������ƫ | C�� | ��ֽ��������ƫ | D�� | ��ֽ����ƫ |
 ����Ϊ2kg��������xOyƽ�����������˶�����x������ٶ�ͼ���y�����λ��ͼ����ͼ��ʾ������˵����ȷ���ǣ�������
����Ϊ2kg��������xOyƽ�����������˶�����x������ٶ�ͼ���y�����λ��ͼ����ͼ��ʾ������˵����ȷ���ǣ�������| A�� | �ʵ�ij��ٶ�Ϊ5m/s | |
| B�� | �ʵ���ٶȵķ��������������ֱ | |
| C�� | �ʵ����ܵĺ�����Ϊ3N | |
| D�� | 2s���ʵ�λ�ƴ�СΪ9m |
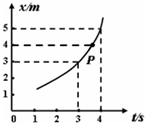
| A�� | �ʵ㾭��;��P������Ӧλ��ʱ���ٶȵ���2m/s | |
| B�� | �ʵ����˶���������3s��3.5s���ʱ����λ�ƴ���1m | |
| C�� | �ʵ����˶���������3s��3.5s���ʱ����λ��С��1m | |
| D�� | �ʵ����˶�������t=3.5sʱ���ٶȵ���2m/s |
 ��ͼ��ʾ���ס�����ͬѧ��ˮƽ������аκӱ����������У�������֮�䲻�����б���������һ���������뷴���������ǣ�������
��ͼ��ʾ���ס�����ͬѧ��ˮƽ������аκӱ����������У�������֮�䲻�����б���������һ���������뷴���������ǣ�������| A�� | �������������Ҷ��������� | |
| B�� | ���������������Լ����� | |
| C�� | �ҵ��������ҶԵ����ѹ�� | |
| D�� | �ҶԵ����ѹ���͵���Լ�֧���� |
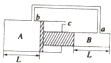 ��ͼ����T���λ��������������ڵ�����ָ���A��B�����֣����������������֮��ΪS1��S2=2��1���������������˵ײ������ΪL=10cm����������a��b��c����С���������ͨ���ֽ�a��b��ϸ�ܣ��ݻ����ƣ����ӣ���֪����ѹǿΪ��0=1.0��105Pa�������¶�ΪT0=300K��������ױڼ���Ħ���Ҳ�©����
��ͼ����T���λ��������������ڵ�����ָ���A��B�����֣����������������֮��ΪS1��S2=2��1���������������˵ײ������ΪL=10cm����������a��b��c����С���������ͨ���ֽ�a��b��ϸ�ܣ��ݻ����ƣ����ӣ���֪����ѹǿΪ��0=1.0��105Pa�������¶�ΪT0=300K��������ױڼ���Ħ���Ҳ�©����