题目内容
4.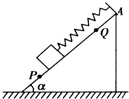 如图所示,在倾角α=60°的斜面上,放一质量为10kg的物体,用k=100N/m的轻质弹簧平行于斜面拉着,物体放在PQ之间任何位置都能处于静止状态,而超过这一范围,物体就会沿斜面滑动,若AP=22cm,AQ=8cm,试求物体与斜面间的最大静摩擦力的大小?(sin60°=$\frac{\sqrt{3}}{2}$,cos60°=$\frac{1}{2}$)
如图所示,在倾角α=60°的斜面上,放一质量为10kg的物体,用k=100N/m的轻质弹簧平行于斜面拉着,物体放在PQ之间任何位置都能处于静止状态,而超过这一范围,物体就会沿斜面滑动,若AP=22cm,AQ=8cm,试求物体与斜面间的最大静摩擦力的大小?(sin60°=$\frac{\sqrt{3}}{2}$,cos60°=$\frac{1}{2}$)
分析 由题,当物体位于P点时,将要向上运动,静摩擦力沿斜面向下达到最大.当物体位于Q点时,物体将向下运动,静摩擦力沿斜面向上达到最大.根据平衡条件和胡克定律列方程求解最大静摩擦力.
解答 解:P、Q两点应是静摩擦力最大的两个临界位置,在P点弹簧处于伸长状态,受力分析如图(1)所示.Ffm=F1-mgsinα…①
在Q点弹簧处于压缩状态,受力分析如图(2)所示.
Ffm=F2+mgsinα…②
设弹簧的原长为x,有F1=k(0.22-x)…③
F2=k(x-0.08)…④
联立①②③④得:2Ffm=F1+F2=k(0.22-0.08)
所以Ffm=$\frac{1}{2}$×100×0.14 N=7 N
答:物体与斜面间的最大静摩擦力的大小是7N.
点评 本题是物体平衡中临界问题,当两物体间恰好发生相对运动时,静摩擦力达到最大是常用的临界条件.

练习册系列答案
相关题目
14.探究感应电流的方向
(1)实验器材:条形磁铁、电流表、线圈、导线、一节干电池(用来查明线圈中电流的流向与电流表中指针偏转方向的关系).
(2)实验现象:如图所示,在四种情况下,将实验结果填入表:
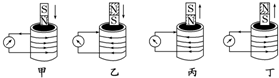
①线圈内磁通量增加时的情况:
②线圈内磁通量减少时的情况:
实验结论:感应电流的磁场总是阻碍 引起感应电流的磁通量的变化.
(1)实验器材:条形磁铁、电流表、线圈、导线、一节干电池(用来查明线圈中电流的流向与电流表中指针偏转方向的关系).
(2)实验现象:如图所示,在四种情况下,将实验结果填入表:

①线圈内磁通量增加时的情况:
| 图号 | 磁场方向 | 感应电流的方向 | 感应电流的磁场方向 |
| 甲 | 向下 | 逆时针(俯视) | 向上 |
| 乙 | 向上 | 顺时针(俯视) | 向下 |
| 图号 | 磁场方向 | 感应电流的方向 | 感应电流的磁场方向 |
| 丙 | 向下 | 顺时针(俯视) | 向下 |
| 丁 | 向上 | 逆时针(俯视) | 向上 |
15.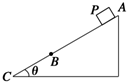 如图所示,固定斜面倾角为θ,整个斜面长分为AB、BC两段,AB=2BC.小物块P(可视为质点)与AB、BC两段斜面间的动摩擦因数分别为μ1、μ2.已知P由静止开始从A点释放,恰好能滑动到C点而停下,则,下列说法正确的是( )
如图所示,固定斜面倾角为θ,整个斜面长分为AB、BC两段,AB=2BC.小物块P(可视为质点)与AB、BC两段斜面间的动摩擦因数分别为μ1、μ2.已知P由静止开始从A点释放,恰好能滑动到C点而停下,则,下列说法正确的是( )
 如图所示,固定斜面倾角为θ,整个斜面长分为AB、BC两段,AB=2BC.小物块P(可视为质点)与AB、BC两段斜面间的动摩擦因数分别为μ1、μ2.已知P由静止开始从A点释放,恰好能滑动到C点而停下,则,下列说法正确的是( )
如图所示,固定斜面倾角为θ,整个斜面长分为AB、BC两段,AB=2BC.小物块P(可视为质点)与AB、BC两段斜面间的动摩擦因数分别为μ1、μ2.已知P由静止开始从A点释放,恰好能滑动到C点而停下,则,下列说法正确的是( )| A. | μ1>tanθ | B. | μ2<tanθ | C. | tanθ=2μ1-μ2 | D. | tanθ=$\frac{{2{μ_1}+{μ_2}}}{3}$ |
12. 表面均匀带电的圆盘水平放置,从靠近圆心O处以初速度V0竖直向上抛出一个质量为m,带电量为-q(q>0)的小球(看作试探电荷),小球上升的最高点为B点,经过A点时速度最大,已知OA=h1,OB=h2,重力加速度为g,取O点电势为零,不计空气阻力,则可以判断( )
表面均匀带电的圆盘水平放置,从靠近圆心O处以初速度V0竖直向上抛出一个质量为m,带电量为-q(q>0)的小球(看作试探电荷),小球上升的最高点为B点,经过A点时速度最大,已知OA=h1,OB=h2,重力加速度为g,取O点电势为零,不计空气阻力,则可以判断( )
 表面均匀带电的圆盘水平放置,从靠近圆心O处以初速度V0竖直向上抛出一个质量为m,带电量为-q(q>0)的小球(看作试探电荷),小球上升的最高点为B点,经过A点时速度最大,已知OA=h1,OB=h2,重力加速度为g,取O点电势为零,不计空气阻力,则可以判断( )
表面均匀带电的圆盘水平放置,从靠近圆心O处以初速度V0竖直向上抛出一个质量为m,带电量为-q(q>0)的小球(看作试探电荷),小球上升的最高点为B点,经过A点时速度最大,已知OA=h1,OB=h2,重力加速度为g,取O点电势为零,不计空气阻力,则可以判断( )| A. | 小球与圆盘带异种电荷 | B. | A点的场强大小为$\frac{mg}{q}$ | ||
| C. | B点的电势为$\frac{m}{2q}$(v02-2gh2) | D. | 若UOA=UAB,则h1<h2-h1 |
19.放在光滑水平面上的物体,仅在两个互相垂直的水平力的共同作用下开始运动,若这两个力分别做了6J和8J的功,则合力做的功为( )
| A. | 2J | B. | 10J | C. | 14J | D. | 48J |
16. 大型游乐场中有一种叫“摩天轮”的娱乐设施,如图所示,坐在其中的游客随轮的转动而做匀速圆周运动,对此有以下说法,其中正确的是( )
大型游乐场中有一种叫“摩天轮”的娱乐设施,如图所示,坐在其中的游客随轮的转动而做匀速圆周运动,对此有以下说法,其中正确的是( )
 大型游乐场中有一种叫“摩天轮”的娱乐设施,如图所示,坐在其中的游客随轮的转动而做匀速圆周运动,对此有以下说法,其中正确的是( )
大型游乐场中有一种叫“摩天轮”的娱乐设施,如图所示,坐在其中的游客随轮的转动而做匀速圆周运动,对此有以下说法,其中正确的是( )| A. | 游客处于一种平衡状态 | B. | 游客做的是一种变加速曲线运动 | ||
| C. | 游客做的是一种匀变速运动 | D. | 游客的机械能守恒 |
13. 一个带负电的橡胶圆盘处在竖直面内,可以绕过其圆心的水平轴高速旋转,当它不转动时,放在它左侧水平轴上的小磁针静止时的指向,如图所示,从左往右看,当橡胶圆盘逆时针高速旋转时,小磁针N极指向( )
一个带负电的橡胶圆盘处在竖直面内,可以绕过其圆心的水平轴高速旋转,当它不转动时,放在它左侧水平轴上的小磁针静止时的指向,如图所示,从左往右看,当橡胶圆盘逆时针高速旋转时,小磁针N极指向( )
 一个带负电的橡胶圆盘处在竖直面内,可以绕过其圆心的水平轴高速旋转,当它不转动时,放在它左侧水平轴上的小磁针静止时的指向,如图所示,从左往右看,当橡胶圆盘逆时针高速旋转时,小磁针N极指向( )
一个带负电的橡胶圆盘处在竖直面内,可以绕过其圆心的水平轴高速旋转,当它不转动时,放在它左侧水平轴上的小磁针静止时的指向,如图所示,从左往右看,当橡胶圆盘逆时针高速旋转时,小磁针N极指向( )| A. | 不偏转 | B. | 在纸面内向左偏 | C. | 在纸面内向右偏 | D. | 向纸面内偏 |
19.如图所示是一个质点做匀变速直线运动x-t图象中的一段,从图中所给的数据可以确定( )


| A. | 质点经过途中P点所对应位置时的速度等于2m/s | |
| B. | 质点在运动过程中在3s~3.5s这段时间内位移大于1m | |
| C. | 质点在运动过程中在3s~3.5s这段时间内位移小于1m | |
| D. | 质点在运动过程中t=3.5s时的速度等于2m/s |
