题目内容
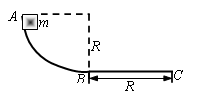
如图所示,在竖直平面内固定着半径为R的半圆形轨道,小球B静止在轨道的最低点,小球A从轨道右端正上方3.5R处由静止自由落下,沿圆弧切线进入轨道后,与小球B发生弹性碰撞。碰撞后B球上升的最高点C,圆心O与C的连线与竖直方向的夹角为60°。若两球均可视为质点,不计一切摩擦,求A、B两球的质量之比mA:mB。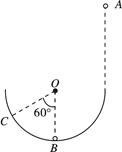
1:5
解析试题分析:小球A从高处静止下落至轨道的最低点,由机械能守恒定律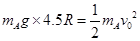
小球A与小球B发生弹性碰撞,由动量守恒定律和能量守恒定律

B球上升到最高点C,由机械能守恒定律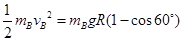
联立解得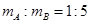
考点:动量守恒定律和机械能守恒 动能定理 功能关系

练习册系列答案
相关题目
某型号的“神舟飞船”顺利发射升空后,在离地面340km的圆轨道上运行了108圈。运行中需要多次进行“轨道维持”。所谓“轨道维持”就是通过控制飞船上发动机的点火时间和推力的大小方向,使飞船能保持在预定轨道上稳定运行。如果不进行轨道维持,由于飞船受轨道上稀薄空气的摩擦阻力,轨道高度会逐渐降低,在这种情况下飞船的动能、重力势能和机械能变化情况将会是( )
| A.动能、重力势能和机械能都逐渐减小 |
| B.重力势能逐渐减小,动能逐渐增大,机械能不变 |
| C.重力势能逐渐增大,动能逐渐减小,机械能不变 |
| D.重力势能逐渐减小,动能逐渐增大,机械能逐渐减小 |

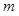 的小物块可从桌面正中心
的小物块可从桌面正中心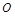 点以初速v0=3m/s沿着与OA成370的方向在桌面上运动直至落地。设动摩擦因数为μ="0.25" ,取g=10m/s2,求
点以初速v0=3m/s沿着与OA成370的方向在桌面上运动直至落地。设动摩擦因数为μ="0.25" ,取g=10m/s2,求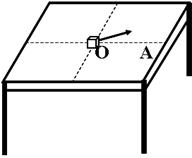
 。
。
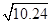 =3.2)
=3.2)
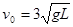 向右匀速行驶。突然,小车因撞到正前方固定障碍物,速度立即变为零,小球以v0为初速度开始在竖直平面内做圆周运动。当小球第一次到达最高点时,地面对车的支持力恰好为零。已知在此过程中,小车一直未动,重力加速度为g。求:
向右匀速行驶。突然,小车因撞到正前方固定障碍物,速度立即变为零,小球以v0为初速度开始在竖直平面内做圆周运动。当小球第一次到达最高点时,地面对车的支持力恰好为零。已知在此过程中,小车一直未动,重力加速度为g。求: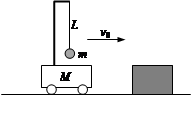
 .求:
.求: