题目内容
(12分)已知某星球的半径为R,有一距星球表面高度h=R处的卫星,绕该星球做匀速圆周运动,测得其周期T=2π 。
。
求:(1)该星球表面的重力加速度g
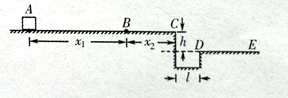
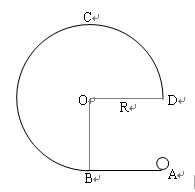
(2)若在该星球表面有一如图所示的装置,其中AB部分为一长为12.8m并以5m/s速度顺时针匀速转动的传送带,BCD部分为一半径为1.6m竖直放置的光滑半圆形轨道,直径BD恰好竖直,并与传送带相切于B点。现将一质量为0.1kg的可视为质点的小滑块无初速地放在传送带的左端A点上,已知滑块与传送带间的动摩擦因数为0.5。试求出到达D点时对轨道的压力大小; (提示: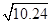 =3.2)
=3.2)
(1)g =" 1.6" m/s2 (2)
解析试题分析:(1)对距星球表面h=R处的卫星(设其质量为m),有: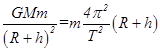 ① (2分)
① (2分)
对在星球表面的物体m′,有: ② (2分)
② (2分)
解得:g =" 1.6" m/s2 (2分)
(2)设滑块从A到B一直被加速,且设到达B点时的速度为VB
则: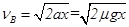 =
=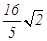 m/s (2分)
m/s (2分)
因VB < 5m/s,故滑块一直被加速 (1分)
设滑块能到达D点,且设到达D点时的速度为VD
则在B到D的过程中,由动能定理:–mg·2R = 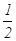 mVD2–
mVD2–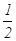 mVB2 (2分)
mVB2 (2分)
解得: ="3.2m/s" (2分)
="3.2m/s" (2分)
而滑块能到达D点的临界速度:V0 =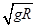 =" 1.6" m/s < VD,即滑块能到达D点。 (1分)
=" 1.6" m/s < VD,即滑块能到达D点。 (1分)
在D点取滑块为研究对象,则有: FN + mg =  (2分)
(2分)
解得:FN = –mg =" 0.48" N (2分)
–mg =" 0.48" N (2分)
考点:万有引力、动能定理、向心力

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
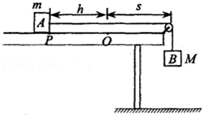
启东小题作业本系列答案如图所示,a、b、c为真空中某电场的一条线上的三点,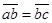 。一带电粒子仅在电场力的作用下由a运动到c,其速度—时间图线如图所示,则( )
。一带电粒子仅在电场力的作用下由a运动到c,其速度—时间图线如图所示,则( )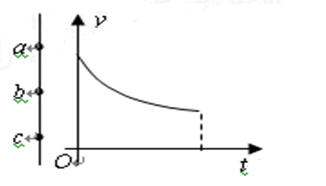
| A.a、b两点的电势差等于b、c两点的电势差 |
| B.a点的电场强度一定大于b点的电场强度 |
| C.a点的电势一定高于c点的电势 |
| D.从a到c带电粒子的电势能减小 |
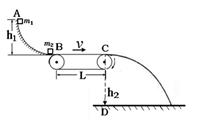
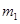 的滑块(可视为质点)自光滑圆弧形槽的顶端A处无初速度的滑下。槽的底端与水平传送带相切于左传导轮顶端的B点,A、B的高度差为
的滑块(可视为质点)自光滑圆弧形槽的顶端A处无初速度的滑下。槽的底端与水平传送带相切于左传导轮顶端的B点,A、B的高度差为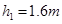 .传导轮半径很小,两个轮之间的距离为
.传导轮半径很小,两个轮之间的距离为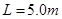 ,滑块与传送带间的动摩擦因数
,滑块与传送带间的动摩擦因数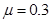 .右端的轮子上沿距离地面的高度为
.右端的轮子上沿距离地面的高度为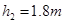 .(
.(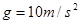 )
)
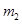 ,传送带静止不转,滑块
,传送带静止不转,滑块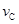 ;
;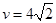 m/s。求滑块
m/s。求滑块 。
。
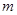 ,从离桌面高为
,从离桌面高为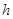 处由静止释放,假设它与桌面碰撞反弹时不损失机械能,但由于受到大小不变的空气阻力的影响(空气浮力不计),每次反弹的高度是它下落时高度的
处由静止释放,假设它与桌面碰撞反弹时不损失机械能,但由于受到大小不变的空气阻力的影响(空气浮力不计),每次反弹的高度是它下落时高度的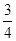 。求:
。求: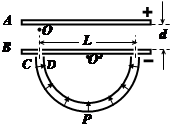
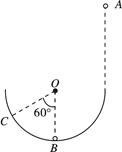
 =0.2,取g=10m/s2,求:
=0.2,取g=10m/s2,求: