题目内容
【题目】用同种材料制成的质量均为M=1kg的形状不同的滑块n个静止在光滑水平面上,编号依次为1、2、3….质量为m=0.1kg的子弹(视为质点)以水平初速度v0=200m/s依次击穿这些滑块后最终保留在第n个滑块中.要求子弹穿过每个滑块的时间都相等,子弹在两滑块间匀速运动的时间也相等且等于子弹穿过一块滑块的时间,这必然导致每个滑块长度不同,滑块间的间距也不同.子弹穿过滑块时受到的水平阻力f=150N并保持恒定.测得子弹穿过编号为1的滑块后滑块的速度变为v=1.5m/s.不考虑子弹在竖直方向上的受力和运动.(滑块不翻转,不计空气阻力)
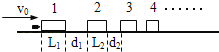
(1)求n
(2)用计算说明子弹刚穿过第N(N<n)块滑块时,第N﹣1块滑块没有追上第N块滑块
【答案】(1)14(2)dN﹣1取最小值是0.2075m.从子弹刚接触N﹣1到刚击穿N的过程N﹣1比N多走的位移,△S=2vt=0.03m,(dN﹣1)min>△S,所以没有追上
【解析】
分析子弹击穿第一块滑块的过程,运用动量守恒定律求解.
第N块刚被击穿时是否被N﹣1块追上,取决于二者静止时的间距dN﹣1是否小于子弹刚接触N﹣1到刚击穿N的过程N﹣1比N多走的位移,分析子弹的运动过程,运用运动学公式求解比较.子弹打穿前13块后,1到13各块的速度均为v,根据系统动量守恒定律和机械能守恒列车等式求解.
(1)子弹击穿第一块滑块的过程,规定向右为正方向,根据动量守恒定律得:
mv0=mv1+Mv
代入数据得:v1=185m/s
由于子弹穿过每个滑块的时间相等、受到的阻力也相等,所以速度的减少量相等,有:
△v=v0﹣v1=15m/s
n![]() ,取n=14
,取n=14
(2)第N块刚被击穿时是否被N﹣1块追上,取决于二者静止时的间距dN﹣1是否小于子弹刚接触N﹣1到刚击穿N的过程N﹣1比N多走的位移.
子弹穿过一块滑块的时间或在两滑块间匀速运动的时间为:t![]() 0.01s
0.01s
子弹击穿第N﹣1块的过程中第N﹣1块的位移为:SN﹣1![]() t=0.0075m
t=0.0075m
子弹击穿N﹣1后匀速飞行的位移为:S′N﹣1=[v0﹣(N﹣1)△v]t=2﹣0.15(N﹣1)m
静止时N﹣1与N的距离为:dN﹣1=SN﹣1+S′N﹣1=2.075﹣0.15(N﹣1)m
当N=13时,dN﹣1取最小值是0.2075m.
从子弹刚接触N﹣1到刚击穿N的过程N﹣1比N多走的位移,如图:
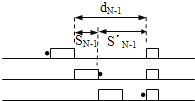
△S=2vt=0.03m,(dN﹣1)min>△S,所以没有追上.

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案