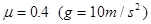题目内容
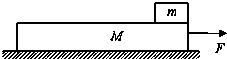 如图所示,有一块木板静止在光滑且足够长的水平面上,木板质量M=4kg,长L=1.4m,木板右端放着一个小滑块.小滑块质量为m=1kg,其尺寸远小于L.小滑块与木板间的动摩擦因数μ=0.4,g=10m/s2.现用恒力F作用于木板M上,若恒力F=22.8N且始终作用于M上,最终使m能从M上滑落,则:m在M上滑动的时间t为多少?
如图所示,有一块木板静止在光滑且足够长的水平面上,木板质量M=4kg,长L=1.4m,木板右端放着一个小滑块.小滑块质量为m=1kg,其尺寸远小于L.小滑块与木板间的动摩擦因数μ=0.4,g=10m/s2.现用恒力F作用于木板M上,若恒力F=22.8N且始终作用于M上,最终使m能从M上滑落,则:m在M上滑动的时间t为多少?分析:根据牛顿第二定律分别求出M和m的加速度,结合位移时间公式,抓住位移之差等于L求出m在M上滑动的时间.
解答:解:对m,根据牛顿第二定律得,a1=
=μg=4m/s2.
对M,有:a2=
=
m/s2=4.7m/s2.
根据
a2t2-
a1t2=L得,
×(4.7-4)t2=1.4
解得t=2s.
答:m在M上滑动的时间为2s.
| μmg |
| m |
对M,有:a2=
| F-μmg |
| M |
| 22.8-0.4×10 |
| 4 |
根据
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解得t=2s.
答:m在M上滑动的时间为2s.
点评:解决本题的关键理清m和M的运动规律,结合牛顿第二定律和运动学公式进行求解.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
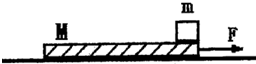 如图所示,有一块木板静止在光滑且足够长的水平面上,木板质量为M=4kg,长为L=1.8m;木板右端放着一小滑块,小滑块质量为m=1kg,其尺寸远小于L.小滑块与木板间的动摩擦因数为μ=0.4.(g=10m/s2)
如图所示,有一块木板静止在光滑且足够长的水平面上,木板质量为M=4kg,长为L=1.8m;木板右端放着一小滑块,小滑块质量为m=1kg,其尺寸远小于L.小滑块与木板间的动摩擦因数为μ=0.4.(g=10m/s2)
 如图所示,有一块木板静止在光滑且足够长的水平面上,木板的质量为M=4㎏,长度为L=1.4m;木板的右端停放着一个小滑块,小滑块质量为m=1㎏,其尺寸远小于木板长度,它与木板间的动摩擦因数为μ=0.4,若滑块所受的最大静摩擦力是相同压力下滑动摩擦力的1.2倍,取g=10m/s2,问:
如图所示,有一块木板静止在光滑且足够长的水平面上,木板的质量为M=4㎏,长度为L=1.4m;木板的右端停放着一个小滑块,小滑块质量为m=1㎏,其尺寸远小于木板长度,它与木板间的动摩擦因数为μ=0.4,若滑块所受的最大静摩擦力是相同压力下滑动摩擦力的1.2倍,取g=10m/s2,问: