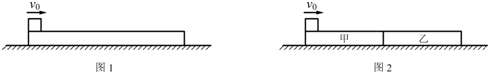题目内容
一滑块(可视为质点)经水平轨道AB进入竖直平面内的四分之一圆弧形轨道BC.已知滑块的质量m=0.50kg，滑块经过A点时的速度vA=5.0m/s,AB长x=4.5m，滑块与水平轨道间的动摩擦因数μ=0.10,圆弧形轨道的半径R=0.50m，滑块离开C点后竖直上升的最大高度h=0.10m.取g=10m/s2.求：
(1)滑块第一次经过B点时速度的大小；
(2)滑块刚刚滑上圆弧形轨道时，对轨道上B点压力的大小；
(3)滑块在从B运动到C的过程中克服摩擦力所做的功.
(1)4.0 m/s (2)21 N (3)1.0 J
解析试题分析：(1)滑块由A到B的过程中，应用动能定理得：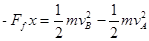
又Ff=μmg
解得：vB="4.0" m/s
(2)在B点，滑块开始做圆周运动，由牛顿第二定律可知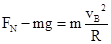
解得轨道对滑块的支持力FN="21" N
根据牛顿第三定律可知，滑块对轨道上B点压力的大小也为21 N
(3)滑块从B经过C上升到最高点的过程中，由动能定理得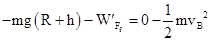
解得滑块克服摩擦力做功W′Ff="1.0" J
考点：动能定理的应用；竖直上抛运动；牛顿第二定律．
点评：本题中第一问也可以根据运动学公式求解，但用动能定理求解不用考虑加速度，过程明显简化；运用动能定理要注意过程的选择，通常运动过程选的越大，解题过程越简化；动能定理比运动学公式适用范围更广，对于曲线运动同样适用．
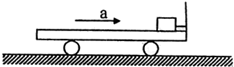一滑块（可视为质点），通过长度不计的细绳拴在小车上，小车上表面光滑．小车由静止开始向右匀加速运动，经过2s，细绳断裂．细绳断裂后，小车的加速度不变，又经过一段时间，滑块从小车左端掉下，在这段时间内，已知滑块相对小车前3s内滑行了4.5m，后3s内滑行了10.5m．求
（2011?安徽一模）如图所示，倾角为30°的光滑斜面与粗糙的水平面平滑连接．现将一滑块（可视为质点）从斜面上A点由静止释放，最终停在水平面上的C点．已知A点距水平面的高度h=0.8m，B点距C点的距离L=2.0m．（滑块经过B点时没有能量损失，g=10m/s2），求：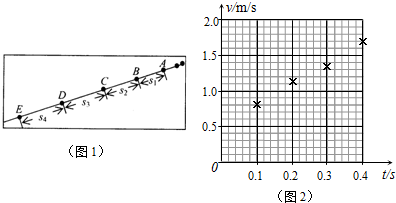
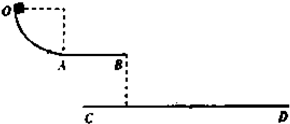如图所示，四分之一圆轨道OA与水平轨道AB相切，它们与另一水平轨道CD在同一竖直面内，圆轨道OA的半径R=0.45m，水平轨道AB长s=1m，OA光滑．质量M=0.2kg的一滑块（可视为质点）从O点由静止释放，滑块与AB间的动摩擦因数μ=0.4．AB与CD的高度差h=0.8m．取g=10/s2．求