题目内容
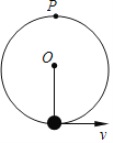
【题目】轻绳一端固定在光滑轴O上，另一端系一质量为m的小球，在最低点给小球一初速度，使其在竖直平面内做圆周运动，且恰好能通过最高点P.下列说法正确的是（ ）
A. 小球在最低点时对绳的拉力为零
B. 小球在最高点时对绳的拉力大小mg
C. 若增大小球的初速度，则过最高点时球对绳的力一定增大
D. 若增大小球的初速度，则在最低点时球对绳的力不一定增大
【答案】C
【解析】
小球恰好通过最高点，可知绳子的拉力为零，靠重力提供向心力，在最低点，靠拉力和重力的合力提供向心力，结合牛顿第二定律分析拉力和小球速度的关系．
A、B、小球恰好通过最高点P，可知在最高点，小球对绳子的拉力为零，在最低点，小球靠拉力和重力的合力提供向心力，拉力大于重力，则拉力不为零，故A，B错误．
C、若增大小球的初速度，则最高点的速度增大，根据牛顿第二定律有：
，可知球对绳子的拉力增大，故C正确．
D、在最低点，根据牛顿第二定律有：
，可知初速度增大，在最低点球对绳子的拉力一定增大，故D错误．
故选C．
练习册系列答案
相关题目
