Question

【题目】如图所示，质量为m的球置于斜面上，被一个竖直挡板挡住。现用一个水平向右的力F拉斜面，使斜面在水平面上向右做加速度为a的匀加速直线运动，忽略一切摩擦，下列说法正确的是（　　）

A. 斜面和挡板对球的弹力的合力等于ma

B. 若加速度足够大，斜面对球的弹力可能为零

C. 若加速度足够小，则竖直挡板对球的弹力可能为零

D. 若加速度不断的增大，斜面对球不仅有弹力，而且该弹力是一个定值

Answer 1

【答案】D

【解析】

A、以小球为研究对象，分析受力情况，

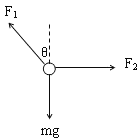
如图：受重力mg、竖直挡板对球的弹力F2和斜面的弹力F1．根据牛顿第二定律知小球所受的合力为ma，即重力、斜面和挡板对球的弹力三个力的合力等于ma，面和挡板对球的弹力的合力不等于ma，故A错误。设斜面的加速度大小为a，根据牛顿第二定律得

竖直方向：F1cosθ＝mg ①

水平方向：F2﹣F1sinθ＝ma，②

由①看出，斜面对球的弹力F1大小不变，与加速度无关，不可能为零。由②看出，若加速度足够小时，F2＝F1sinθ＝mgtanθ≠0．故BC错误。若F增大，a增大，斜面的弹力F1大小不变。故D正确。故选：D。