��Ŀ����
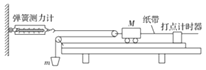
����Ŀ����ͼ��ʾ�����Ϊ![]() �Ĵֲ�ƽֱ������뾶Ϊr�Ĺ⻬Բ��������У��е�Ϊb���������������ֱƽ����. һ����Ϊm��С����ӵ�����������ΪH=3r��d�������»�����Բ�����������С�������ߵ�aˮƽ�ɳ���ǡ�û��е�������Բ��O�ȸߵ�c��. ��֪Բ����͵�Ϊe�㣬�������ٶ�Ϊg�����ƿ�������. ��
�Ĵֲ�ƽֱ������뾶Ϊr�Ĺ⻬Բ��������У��е�Ϊb���������������ֱƽ����. һ����Ϊm��С����ӵ�����������ΪH=3r��d�������»�����Բ�����������С�������ߵ�aˮƽ�ɳ���ǡ�û��е�������Բ��O�ȸߵ�c��. ��֪Բ����͵�Ϊe�㣬�������ٶ�Ϊg�����ƿ�������. ��
��1��С������a��ɳ��Ķ��ܣ�
����С������e���Բ�����ѹ���Ĵ�С��
��3��С������б��֮��Ķ�Ħ������. �����������Ա������ţ�

���𰸡���1��![]() ����2��F��=6mg����3��
����2��F��=6mg����3��![]()
��������
��1��С�����a��ɳ�����ƽ���˶���
ˮƽ����![]()
��ֱ����![]()
��ã�![]()
С������a��ɳ��Ķ���![]()
��2����С������e��ʱ�ٶ�Ϊ![]() ���ɻ�е���غ㶨�ɵã�
���ɻ�е���غ㶨�ɵã�
![]()
����͵���ţ�ٵڶ����ɣ�![]()
��ţ�ٵ������ɵã�F��=F
��ã�F��=6mg
��3��bd֮�䳤��ΪL���ɼ��ι�ϵ�ã�![]()
��d����͵�e�����У��ɶ��ܶ���![]()
���![]()

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ