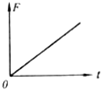题目内容
2.如图a所示质量为m的物体放在倾角为θ的斜面上.
(1)若物体静止在倾角为θ的斜面上,分析物体的受力情况,并求出它们的大小.
(2)若物体在倾角为θ斜面上恰好能匀速下滑,求物体与斜面的动摩擦因数.
(3)如图b所示,物体自O点由静止开始做匀加速直线运动,A、B、C、D是轨迹上的四点,测得AB=2m,BC=3m,CD=4m,且物体通过AB、BC、CD所用时间相等,求OA之间的距离为多少?
分析 (1)对物体受力分析,根据共点力平衡求出支持力和摩擦力的大小.
(2)结合支持力和滑动摩擦力的大小,根据滑动摩擦力公式求出动摩擦因数的大小.
(3)根据连续相等时间内的位移之差是一恒量求出加速度的表达式,根据某段时间内的平均速度等于中间时刻的瞬时速度求出B点的瞬时速度,结合速度位移公式求出OB的距离,从而求出OA间的距离.
解答 解:(1)受力分析如图,
物体受到斜面的支持力:N=mgcosθ
物体受到斜面的静摩擦力:f=mgsinθ
(2)物体匀速下滑,所以物体受到斜面的滑动摩擦力:f=mgsinθ,
又f=μN
故μ=$\frac{f}{N}$=tanθ
(3)设物体通过AB、BC、CD所用的时间均为t,由匀变速直线运动的规律相邻相等的时间内位移之差为常数,即△x=at2可得物体的加速度a的大小为:
a=$\frac{BC-AB}{{t}^{2}}=\frac{3-2}{{t}^{2}}=\frac{1}{{t}^{2}}$,
因某段时间内的平均速度等于中间时刻的瞬时速度,所以物体经过B点时的瞬时速度为:${v}_{B}=\frac{AC}{2t}=\frac{5}{2t}$,
再由${{v}_{B}}^{2}=2a{x}_{OB}$可得,OB两点间的距离为:${x}_{OB}=\frac{{{v}_{B}}^{2}}{2a}=\frac{25}{4{t}^{2}}•\frac{{t}^{2}}{2}=3.125m$.
所以O与A间的距离为:xOA=xOB-AB=(3.125-2)m=1.125m.
答:(1)支持力的大小为mgcosθ,摩擦力的大小为mgsinθ;
(2)物体与斜面的动摩擦因数为tanθ;
(3)OA之间的距离为1.125m.
点评 本题考查了共点力平衡和运动学公式和推论的运用,对于第二问,关键通过共点力平衡求出支持力和滑动摩擦力的大小,对于第三问,运用推论求解比较简捷.

| A. | 点电荷周围的电场可视为匀强电场 | |
| B. | 平行板电容器之间的电场除边缘外可视为匀强电场 | |
| C. | 直线电流周围的磁场可视为匀强磁场 | |
| D. | 环形电流周围的磁场可视为匀强磁场 |
 如图所示,一个质点做圆周运动,A、B、C是其轨迹上的三点.下列说法正确的是( )
如图所示,一个质点做圆周运动,A、B、C是其轨迹上的三点.下列说法正确的是( )| A. | 质点A可能做匀速运动 | |
| B. | 质点一定做变速运动 | |
| C. | 质点受到的合力可能等于零 | |
| D. | 质点经过A、C两点时的速度可能相同 |
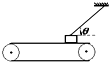 如图所示,质量为m的物体用细绳拴住放在水平粗糙传送带上,物体距传送带左端距离为L,稳定时绳与水平方向的夹角为θ.当传送带分别以v1、v2的速度作逆时针转动时(v1<v2),绳中的拉力分别为Fl、F2;若剪断细绳时,物体一直匀加速运动到达左端时,所用的时间分别为tl、t2,达到左端速度分别为v′1、v′2.则下列说法正确的是( )
如图所示,质量为m的物体用细绳拴住放在水平粗糙传送带上,物体距传送带左端距离为L,稳定时绳与水平方向的夹角为θ.当传送带分别以v1、v2的速度作逆时针转动时(v1<v2),绳中的拉力分别为Fl、F2;若剪断细绳时,物体一直匀加速运动到达左端时,所用的时间分别为tl、t2,达到左端速度分别为v′1、v′2.则下列说法正确的是( )| A. | F1=F2 | B. | Fl<F2 | C. | v′1=v′2 | D. | tl>t2 |
 如图所示,用一根细线一端固定在一光滑斜面顶上,另一端系一可视为质点的小球m,设线的张力大小为F、斜面对小球的支持力大小为FN,光滑斜面在外力作用下向右做加速度增大的加速运动,(细线不会被拉断)则F和FN随α变化的情况是( )
如图所示,用一根细线一端固定在一光滑斜面顶上,另一端系一可视为质点的小球m,设线的张力大小为F、斜面对小球的支持力大小为FN,光滑斜面在外力作用下向右做加速度增大的加速运动,(细线不会被拉断)则F和FN随α变化的情况是( )| A. | F一直减小 | B. | F先增大后减小 | C. | FN一直增大 | D. | FN先减小后不变 |
| A. | 先放开纸带让重物下落,再接通打点计时器的电源 | |
| B. | 必须用秒表测出重锤下落的时间 | |
| C. | 先取下固定在重物上的打好点的纸带,再切断打点计时器的电源 | |
| D. | 选取重物时,其质量适当大点,可以减小因阻力而产生的误差 |
 传感器是把非电物理量(如高度、温度、压力等)的变化转换成电学量(如电压、电流、电容等)变化的一种元件,它在自动控制中有着广泛的应用.如图是一种测定液面高度的电容式传感器的示意图.金属棒与导电液体构成一个电容器,将金属棒和导电液体分别与直流电源的两极相连接,从电容C和导电液与金属棒间的电压U的变化就能反映液面的升降情况,即( )
传感器是把非电物理量(如高度、温度、压力等)的变化转换成电学量(如电压、电流、电容等)变化的一种元件,它在自动控制中有着广泛的应用.如图是一种测定液面高度的电容式传感器的示意图.金属棒与导电液体构成一个电容器,将金属棒和导电液体分别与直流电源的两极相连接,从电容C和导电液与金属棒间的电压U的变化就能反映液面的升降情况,即( )| A. | 电源接通,若此后电容C减小,反映h增大 | |
| B. | 电源接通,若此后电容C增大,反映h增大 | |
| C. | 电源接通再断开,若此后电压U减小,反映h减小 | |
| D. | 电源接通再断开,若此后电压U减小,反映h增大 |
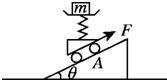 如图所示,质量为60kg的物体放在安装在小车上的水平磅秤上,小车与磅秤的总质量为40kg,小车在平行于斜面的拉力F作用下沿斜面向上减速运动,物体与磅秤之间保持相对静止,斜面体静止在水平地面上,磅秤的读数为564N;小车与斜面间的动摩擦因数为0.8.斜面倾角θ=37°(g取10m/s2).求:
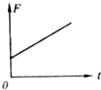
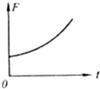
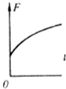
如图所示,质量为60kg的物体放在安装在小车上的水平磅秤上,小车与磅秤的总质量为40kg,小车在平行于斜面的拉力F作用下沿斜面向上减速运动,物体与磅秤之间保持相对静止,斜面体静止在水平地面上,磅秤的读数为564N;小车与斜面间的动摩擦因数为0.8.斜面倾角θ=37°(g取10m/s2).求: 如图所示,物块a放在轻弹簧上,物块b放在物块a上静止不动.当用力F使物块b竖直向上作匀加速直线运动,在下面所给的四个图象中.能反映物块b脱离物块a前的过程中力F随时间t变化规如图所示,物块a放在轻弹簧上,物块b放在物块a上静止不动.当用力F使物块b竖直向上作匀加速直线运动,在下面所给的四个图象中.能反映物块b脱离物块a前的过程中力F随时间t变化规律的是( )
如图所示,物块a放在轻弹簧上,物块b放在物块a上静止不动.当用力F使物块b竖直向上作匀加速直线运动,在下面所给的四个图象中.能反映物块b脱离物块a前的过程中力F随时间t变化规如图所示,物块a放在轻弹簧上,物块b放在物块a上静止不动.当用力F使物块b竖直向上作匀加速直线运动,在下面所给的四个图象中.能反映物块b脱离物块a前的过程中力F随时间t变化规律的是( )