题目内容
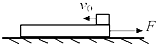 如图所示,质量为2kg的木板B静止在光滑水平面上,质量为1kg可视为质点的木块A以水平速度v0=2m/s从右端向左滑上木板.木块与木板间的动摩擦因数为μ=0.5,此时有一水平向右的力F=10N作用在长木板上.g取10m/s2.
如图所示,质量为2kg的木板B静止在光滑水平面上,质量为1kg可视为质点的木块A以水平速度v0=2m/s从右端向左滑上木板.木块与木板间的动摩擦因数为μ=0.5,此时有一水平向右的力F=10N作用在长木板上.g取10m/s2.(1)求开始时木块A和木板B各自的加速度大小;
(2)若木板足够长,求从木块滑上木板到木块和木板速度相等所经历的时间;
(3)要使木块不从木板上滑落,求木板的最小长度.
分析:(1)对木块和木板分别受力分析,根据牛顿第二定律列方程求解加速度;
(2)A物体先向左减速到0后再向右加速,由速度时间公式求所用时间;
(3)要使木块不滑下,应使木板的长度至少等于木板和木块在这段时间内的位移差.
(2)A物体先向左减速到0后再向右加速,由速度时间公式求所用时间;
(3)要使木块不滑下,应使木板的长度至少等于木板和木块在这段时间内的位移差.
解答:解:(1)对木块和木板分别受力分析
对A分析 a1=μg=0.5×10=5m/s2
对B分析 F-μmg=2ma2 a2=
=2.5m/s2
(2)A物体向左减速到v=0时所用时间为t1
vA=v0-μgt1 得:t1=0.4s
此时B物体 vB=a2t1 vB=1m/s
A、B一起向右加速到共速时间为t2
a1t2=vB+a2t2 t2=0.4s
t总=t1+t2=0.8s
(3)A物体向左 xA=
xA=0.4m
B物体向右 xB=
a2t12=
×2.5×0.42=0.2m
A、B相反运动过程中的相对位移为△x1=0.4+0.2=0.6m
A、B一起向右过程中A、B的位移差为△x2=xB′-xA′=(VBt2+
a2t22)-
a1t22=(1×0.4+
×2.5×0.42)-
×5×0.42=0.2m
要使木块不滑下,木板最小长度为△x总=△x1+△x2=0.8m
答:(1)求开始时木块A和木板B各自的加速度大小分别为5m/s2和2.5m/s2;
(2)若木板足够长,从木块滑上木板到木块和木板速度相等所经历的时间为0.8s;
(3)要使木块不从木板上滑落,木板的最小长度为0.8m.
对A分析 a1=μg=0.5×10=5m/s2
对B分析 F-μmg=2ma2 a2=
| 10-0.5×1×10 |
| 2 |
(2)A物体向左减速到v=0时所用时间为t1
vA=v0-μgt1 得:t1=0.4s
此时B物体 vB=a2t1 vB=1m/s
A、B一起向右加速到共速时间为t2
a1t2=vB+a2t2 t2=0.4s
t总=t1+t2=0.8s
(3)A物体向左 xA=
| v02 |
| 2μg |
B物体向右 xB=
| 1 |
| 2 |
| 1 |
| 2 |
A、B相反运动过程中的相对位移为△x1=0.4+0.2=0.6m
A、B一起向右过程中A、B的位移差为△x2=xB′-xA′=(VBt2+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
要使木块不滑下,木板最小长度为△x总=△x1+△x2=0.8m
答:(1)求开始时木块A和木板B各自的加速度大小分别为5m/s2和2.5m/s2;
(2)若木板足够长,从木块滑上木板到木块和木板速度相等所经历的时间为0.8s;
(3)要使木块不从木板上滑落,木板的最小长度为0.8m.
点评:本题属于连接体问题,关键是隔离法受力分析然后正确运用牛顿第二定律求出各自的加速度.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
 (2011?郑州模拟)如图所示,A、B两球完全相同,质量均为m,用两根等长的细线,悬挂在升降机的天花板上的O点,两球之间连着一根劲度系数为k的轻质弹簧.当升降机以加速度a竖直向上加速运动时,两根细线之间的夹角为θ.则弹簧的长度与原长相比缩短了( )
(2011?郑州模拟)如图所示,A、B两球完全相同,质量均为m,用两根等长的细线,悬挂在升降机的天花板上的O点,两球之间连着一根劲度系数为k的轻质弹簧.当升降机以加速度a竖直向上加速运动时,两根细线之间的夹角为θ.则弹簧的长度与原长相比缩短了( ) (1)在做“用单摆测定重力加速度”的实验中,有人提出以下几点建议:
(1)在做“用单摆测定重力加速度”的实验中,有人提出以下几点建议: ,量程为1mA,内阻rg约为100Ω.要求测量其内阻.可选用的器材有:电阻箱R0,最大阻值为99999.9Ω;滑动变阻器甲,最大阻值为10kΩ;滑动变阻器乙,最大阻值为2kΩ;电源E1,电动势约为2V,内阻不计;电源E2,电动势约为6V,内阻不计;开关2个,导线若干.
,量程为1mA,内阻rg约为100Ω.要求测量其内阻.可选用的器材有:电阻箱R0,最大阻值为99999.9Ω;滑动变阻器甲,最大阻值为10kΩ;滑动变阻器乙,最大阻值为2kΩ;电源E1,电动势约为2V,内阻不计;电源E2,电动势约为6V,内阻不计;开关2个,导线若干. 满偏;c.合上S2,调节R1使
满偏;c.合上S2,调节R1使 半偏,此时可认为的
半偏,此时可认为的 的内阻rg=R1.试问:
的内阻rg=R1.试问: (1)下列说法正确的是
(1)下列说法正确的是 与劲度系数为K的轻质弹簧连接,右端与劲度系数为2K的轻质弹簧连接,左右两弹簧原长均为L0,弹簧的另一端均固定在墙壁上.将物体拉离平衡位置,放手后,物体在光滑水平面上往复运动,证明物体的运动是简谐运动并求简谐运动的平衡位置.
与劲度系数为K的轻质弹簧连接,右端与劲度系数为2K的轻质弹簧连接,左右两弹簧原长均为L0,弹簧的另一端均固定在墙壁上.将物体拉离平衡位置,放手后,物体在光滑水平面上往复运动,证明物体的运动是简谐运动并求简谐运动的平衡位置. (1)有一游标卡尺,主尺的最小分度是1mm,游标上有20个小的等分刻度.用它测量一小球的直径,如图1所示的读数是
(1)有一游标卡尺,主尺的最小分度是1mm,游标上有20个小的等分刻度.用它测量一小球的直径,如图1所示的读数是
 一有界匀强磁场区域如图所示,质量为m、电阻为R的长方形矩形线圈abcd边长分别为L和2L,线圈一半在磁场内,一半在磁场外,t0时刻磁场开始均匀减小,磁感强度B随时间t的变化关系为B=B0-kt,线圈中产生感应电流,仅在磁场力作用下从静止开始运动,求:
一有界匀强磁场区域如图所示,质量为m、电阻为R的长方形矩形线圈abcd边长分别为L和2L,线圈一半在磁场内,一半在磁场外,t0时刻磁场开始均匀减小,磁感强度B随时间t的变化关系为B=B0-kt,线圈中产生感应电流,仅在磁场力作用下从静止开始运动,求: