题目内容
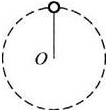 轻杆一端固定质量为m的小球,以另一端O为圆心,使小球在竖直平面内作半径为R的圆周运动,则( )
轻杆一端固定质量为m的小球,以另一端O为圆心,使小球在竖直平面内作半径为R的圆周运动,则( )分析:轻杆带着物体做圆周运动,只要物体能够到达最高点就可以了,在最高点和最低点时物体的重力与杆对球的作用力的合力作为向心力.
解答:解:A、杆既可以提供拉力,又可以提供支持力,所以小球到达最高点时的最小速度可以等于零,故A错误;
B、小球在最高点时,如果速度恰好为
,则此时恰好只有重力作为它的向心力,杆和球之间没有作用力,所以小球过最高点时,杆所受弹力可以为零,故B正确;
C、当v>
时,根据牛顿第二定律得:
T+mg=m
杆对球产生向下的拉力,故C正确;
D、当v<
时,根据牛顿第二定律得:
mg-T=m
杆对小球产生向上的弹力,故D错误.
故选:BC
B、小球在最高点时,如果速度恰好为
| gL |
C、当v>
| gL |
T+mg=m
| v2 |
| L |
杆对球产生向下的拉力,故C正确;
D、当v<
| gL |
mg-T=m
| v2 |
| L |
杆对小球产生向上的弹力,故D错误.
故选:BC
点评:杆的模型和绳的模型是在高中常遇到的两种基本模型,这两种模型不一样,杆在最高点的速度可以为零,而绳在最高点时的速度必须大于或等于最小速度.

练习册系列答案
相关题目
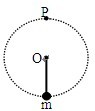 如图所示,长为L的轻杆一端固定质量为m的小球,另一端有固定转轴O,现使小球在竖直平面内做圆周运动,P为圆周的最高点,若小球通过圆周轨道最低点时的速度大小为
如图所示,长为L的轻杆一端固定质量为m的小球,另一端有固定转轴O,现使小球在竖直平面内做圆周运动,P为圆周的最高点,若小球通过圆周轨道最低点时的速度大小为
|
| A、小球不能到达P点 | ||
B、小球到达P点时的速度大于
| ||
| C、小球能到达P点,且在P点受到轻杆向下的拉力 | ||
| D、小球能到达P点,且在P点受到轻杆向上的支持力 |
 如图所示,长为L的轻杆一端固定质量为m的小球,另一端可绕固定转轴0无摩擦转动.静止在最低点P的小球瞬间获得一水平初速度后在竖直面内做完整的圆周运动,Q为最高点.则以下说法正确的是( )
如图所示,长为L的轻杆一端固定质量为m的小球,另一端可绕固定转轴0无摩擦转动.静止在最低点P的小球瞬间获得一水平初速度后在竖直面内做完整的圆周运动,Q为最高点.则以下说法正确的是( )| A、小球通过P点时处于平衡状态 | B、小球在P点时可能对轻杆有向上的压力作用 | C、小球在Q点时可能对轻杆没有作用力 | D、轻杆在小球通过Q点时对小球的作用力一定小于轻杆在小球通过p点时对小球 的作用力 |
 长为L的轻杆一端固定质量为m的小球,另一端可绕固定光滑水平转轴O转动.现使小球在竖直平面内做圆周运动,C为圆周的最高点,若小球通过圆周最低点D的速度大小为
长为L的轻杆一端固定质量为m的小球,另一端可绕固定光滑水平转轴O转动.现使小球在竖直平面内做圆周运动,C为圆周的最高点,若小球通过圆周最低点D的速度大小为 如图所示,长为L的轻杆一端固定质量为m的小球,另一端有固定转轴O.现使小球在竖直平面内做圆周运动,P为圆周轨道的最高点,若小球通过圆周轨道最低点时的速度大小为
如图所示,长为L的轻杆一端固定质量为m的小球,另一端有固定转轴O.现使小球在竖直平面内做圆周运动,P为圆周轨道的最高点,若小球通过圆周轨道最低点时的速度大小为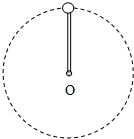 如图所示,一长为L轻杆一端固定质量为m的小球,以另一端O为圆心,使得小球在竖直平面内做圆周运动,小球在最高点的速率为v,以下说法正确的是( )
如图所示,一长为L轻杆一端固定质量为m的小球,以另一端O为圆心,使得小球在竖直平面内做圆周运动,小球在最高点的速率为v,以下说法正确的是( )