题目内容
 长为L的轻杆一端固定质量为m的小球,另一端可绕固定光滑水平转轴O转动.现使小球在竖直平面内做圆周运动,C为圆周的最高点,若小球通过圆周最低点D的速度大小为
长为L的轻杆一端固定质量为m的小球,另一端可绕固定光滑水平转轴O转动.现使小球在竖直平面内做圆周运动,C为圆周的最高点,若小球通过圆周最低点D的速度大小为| 6gL |
分析:根据动能定理求出小球在C点的速度,小球在C点的临界速度为零,根据牛顿第二定律求出在最高点杆子的作用力表现为什么力.
解答:解:A、B根据动能定理得,-mg?2L=
m
-
m
,又vD=
,
解得vC=
.故A、B错误.
C、D小球在最高点时,设杆子对小球有支持力,则
mg-F=m
,解得F=-mg,负号表示F向下,故杆子表现为拉力,大小为mg.故C错误,D正确.
故选D
| 1 |
| 2 |
| v | 2 C |
| 1 |
| 2 |
| v | 2 D |
| 6gL |
解得vC=
| 2gL |
C、D小球在最高点时,设杆子对小球有支持力,则
mg-F=m
| ||
| L |
故选D
点评:本题综合考查了动能定理以及牛顿第二定律,关键搞清向心力的来源,运用牛顿定律进行求解.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
 如图所示,长为L的轻杆一端固定质量为m的小球,另一端可绕固定转轴0无摩擦转动.静止在最低点P的小球瞬间获得一水平初速度后在竖直面内做完整的圆周运动,Q为最高点.则以下说法正确的是( )
如图所示,长为L的轻杆一端固定质量为m的小球,另一端可绕固定转轴0无摩擦转动.静止在最低点P的小球瞬间获得一水平初速度后在竖直面内做完整的圆周运动,Q为最高点.则以下说法正确的是( )| A、小球通过P点时处于平衡状态 | B、小球在P点时可能对轻杆有向上的压力作用 | C、小球在Q点时可能对轻杆没有作用力 | D、轻杆在小球通过Q点时对小球的作用力一定小于轻杆在小球通过p点时对小球 的作用力 |
 如图所示,长为L的轻杆一端固定质量为m的小球,另一端有固定转轴O.现使小球在竖直平面内做圆周运动,P为圆周轨道的最高点,若小球通过圆周轨道最低点时的速度大小为
如图所示,长为L的轻杆一端固定质量为m的小球,另一端有固定转轴O.现使小球在竖直平面内做圆周运动,P为圆周轨道的最高点,若小球通过圆周轨道最低点时的速度大小为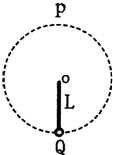 如图所示,长为L的轻杆一端固定一质量为m的小球,另一端有固定转动轴O,杆可在竖直平面内绕轴O无摩擦地转动.已知小球通过最高点P时,速度的大小为
如图所示,长为L的轻杆一端固定一质量为m的小球,另一端有固定转动轴O,杆可在竖直平面内绕轴O无摩擦地转动.已知小球通过最高点P时,速度的大小为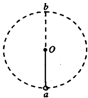 如图所示,长为L 的轻杆一端固定质量为m的小球,另一端有固定转轴O.现使小球在竖直平面内做圆周运动,b为圆周运动的最高点.若小球通过圆周轨道最低点时的速度大小为
如图所示,长为L 的轻杆一端固定质量为m的小球,另一端有固定转轴O.现使小球在竖直平面内做圆周运动,b为圆周运动的最高点.若小球通过圆周轨道最低点时的速度大小为