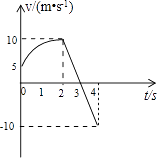Question

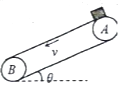
【题目】放在倾角30°斜面上的一物块，受到平行斜面向上的推力F的作用，F的大小与时间t的关系和物块速度v与时间t的关系如图所示，试根据此两图线求出物块的质量m和物块与斜面之间的动摩擦因数μ分别为多少？（g=10m/s2 ， sin30°= ，cos30°= ，结果可以用根式表示）

Answer 1

【答案】解：由v﹣t图象知：2s～4s物块做匀加速运动，加速度为：

a= = ═3m/s2；

根据牛顿第二定律得：

F1﹣f﹣mgsin30°=ma

又 f=μFN=μmgcos30°

即得：F1﹣μmgcos30°﹣mgsin30°=ma

将 F1=3N，代入上式得：3﹣μmgcos30°﹣mgsin30°=3m…①

4s～6s物块做匀速直线运动，有：F2=μmgcos30°+mgsin30°

将F2=2N，代入上式得：μmgcos30°+mgsin30°=2N…②

联立①②解得：m= kg，μ= ．

答：物块的质量m和物块与斜面之间的动摩擦因数μ分别为 kg和 ．

【解析】加速度是联系运动与受力的桥梁即是连接v-t图像，F-t 图像的桥梁，但要注意在这个F-t图像中的F不是合外力而是物体所受力中的一个力，对物体在运动过程中有正确的受力分析再结合牛顿第二定律即可求解。

【考点精析】本题主要考查了V-t图象的相关知识点，需要掌握v-t图像：①在速度图像中，可以读出物体在任何时刻的速度；②在速度图像中，物体在一段时间内的位移大小等于物体的速度图像与这段时间轴所围面积的值；③在速度图像中，物体在任意时刻的加速度就是速度图像上所对应的点的切线的斜率；④图线与横轴交叉，表示物体运动的速度反向；⑤图线是直线表示物体做匀变速直线运动或匀速直线运动;图线是曲线表示物体做变加速运动才能正确解答此题．