Question

【题目】由三颗星体构成的系统，忽略其它星体对它们的作用，其中有一种运动形式：三颗星体在相互之间的万有引力作用下，分别位于一等边三角形的三个顶点上，绕某一共同的圆心O在等边三角形所在的平面内做角速度相同的圆周运动，如图所示。已知A星体质量为2m，B、C两星体的质量均为m，AD为BC边的中垂线。下列说法正确的是（　　）

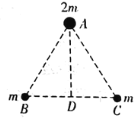
A.圆心O在中垂线AD的中点处B.A星体的轨道半径最大

C.A星体的线速度最大D.A星体的加速度最大

Answer 1

【答案】A

【解析】

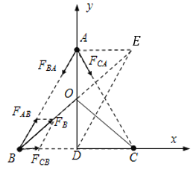
A．对B星体受力分析，如下图所示，，，可知，，以两力为邻边，做平行四边形；以AB边和BD边为邻边，做平行四边形ABDE，则两平行四边形相似，两对角线重合，即的方向指向O点；同理，C星体所受合力也必然指向O点。而根据受力的对称性，A星体所受合力也必然指向O点。所以O点是他们共同的圆心；因为O点是平行四边形ABDE两对角线的交点，故O点在中垂线AD的中点处，A正确；

B．既然它们的圆心在中垂线AD的中点O处，则根据几何关系，A星体的轨道半径最小，B错误；

C．A星B星C星同轴传动，角速度相等，根据可知，A星的线速度最小，C错误；

D．A星B星C星同轴传动，角速度相等，根据可知，A星的加速度最小，D错误。

故选A。