题目内容
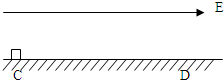一质量为m的小滑块带正电，电荷量为q，与绝缘水平面间的动摩擦因数为μ．空间存在水平向右的匀强电场，电场强度为E．小滑块从C点由静止释放沿直线向D点运动，C、D两点间的距离为S，滑块的带电量不变，重力加速度g．（1）求滑块运动到D点时的速度大小v；
（2）在该空间再加一垂直纸面向里的水平匀强磁场，磁感应强度为B，若滑块从C点由静止释放，运动到D点时恰好离开水平面，求离开水平面时的速度大小υ1和此过程中摩擦力对滑块所做的功W．
分析：（1）由动能定理可以求出滑块到D点的速度．
（2）当滑块受到的洛伦兹力等于滑块的重力时，滑块开水离开水平面，根据洛伦兹力与重力相等可以求出滑块速度；应用动能定理可以求出摩擦力所做的功．
（2）当滑块受到的洛伦兹力等于滑块的重力时，滑块开水离开水平面，根据洛伦兹力与重力相等可以求出滑块速度；应用动能定理可以求出摩擦力所做的功．
解答：解：（1）从C到D过程中，由动能定理得：
qES-μmgS=
mv2-0，
解得：v=
；
（2）当洛伦兹力等于滑块重力时，滑块开始离开水平面，
由平衡条件得，qBv1=mg，解得v1=
，
从C到D过程中，由动能定理得：qES+W=
mv12-0，
解得：W=
-qES；
答：（1）求滑块运动到D点时的速度大小为
．
（2）滑块离开水平面时的速度大小为
，
此过程中摩擦力对滑块所做的功
-qES．
qES-μmgS=
| 1 |
| 2 |
解得：v=
|
（2）当洛伦兹力等于滑块重力时，滑块开始离开水平面，
由平衡条件得，qBv1=mg，解得v1=
| mg |
| qB |
从C到D过程中，由动能定理得：qES+W=
| 1 |
| 2 |
解得：W=
| m3g2 |
| 2q2B2 |
答：（1）求滑块运动到D点时的速度大小为
|
（2）滑块离开水平面时的速度大小为
| mg |
| qB |
此过程中摩擦力对滑块所做的功
| m3g2 |
| 2q2B2 |
点评：要掌握应用动能定理解题的方法与步骤，（1）也可以应用牛顿第二定律与运动学公式求解．
练习册系列答案
相关题目
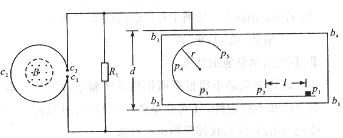
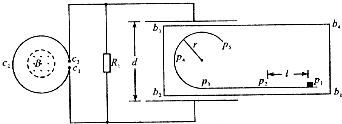（2009?四川）如图所示，直线形挡板p1p2p3与半径为r的圆弧形挡板p3p4p5平滑连接并安装在水平台面b1b2b3b4上，挡板与台面均固定不动．线圈c1c2c3的匝数为n，其端点c1、c3通过导线分别与电阻R1和平行板电容器相连，电容器两极板间的距离为d，电阻R1的阻值是线圈c1c2c3阻值的2倍，其余电阻不计，线圈c1c2c3内有一面积为S、方向垂直于线圈平面向上的匀强磁场，磁场的磁感应强度B随时间均匀增大．质量为m的小滑块带正电，电荷量始终保持为q，在水平台面上以初速度v0从p1位置出发，沿挡板运动并通过p5位置．若电容器两板间的电场为匀强电场，p1、p2在电场外，间距为L，其间小滑块与台面的动摩擦因数为μ，其余部分的摩擦不计，重力加速度为g．
如图所示，在光滑水平面上有一足够长的绝缘平板，质量为M，上表面粗糙，向右运动的速度为V0，平面上方有垂直纸面向里的匀强磁场，磁感应强度大小为B．现在平板右端无初速释放一质量为m的小滑块，小滑块所带电量为+q．试讨论在以后的运动过程中：
