Question

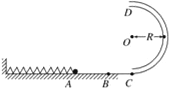
【题目】如图所示，一内壁光滑的细管弯成半径为R=0.4m的半圆形轨道CD，竖直放置，其内径略大于小球的直径，水平轨道与竖直半圆轨道在C点相切．置于水平轨道上的弹簧左端与竖直墙壁相连，B处为弹簧处于自然状态时右端的位置．将一个质量为m=0.8kg的小球放在弹簧的右侧后，用力向左侧推小球而压缩弹簧至A处，然后将小球由静止释放，已知小球运动到C处的速度为5m/s．水平轨道以B处为界，左侧AB段长为x=0.5m，与小球的动摩擦因数为μ=0.4，右侧BC段光滑．g=10m/s2，求：

（1）静止释放小球时弹簧储存的弹性势能．

（2）小球运动到轨道最高处D点时轨道对小球的弹力．

Answer 1

【答案】（1）11.6J．（2）10N，方向竖直向上．

【解析】解：（1）小球由A处运动到C处的过程，根据能量守恒定律得弹簧储存的弹性势能为：

Ep=+μmgx

代入数据解得：Ep=11.6J

（2）小球从C到D的过程，由机械能守恒定律得：

=2mgR+

代入解得：vD=3m/s

由于vD＞==2m/s，所以小球在D处对轨道上壁有压力，对小球，由牛顿第二定律得：

N+mg=

代入解得：N=10N

根据牛顿第三定律，小球对轨道的压力大小为：N′=N=10N，方向竖直向上．