��Ŀ����
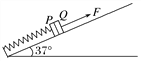
����Ŀ����ͼ��ʾ����ֱƽ������һ�⻬ֱ��AB������ˮƽ����ļн�Ϊ��(0�������90��)��һ����Ϊm��СԲ������ֱ���ϣ���СԲ��ʩ��һ�����ֱƽ��ƽ�еĺ���F������A���ɾ�ֹ�ͷţ��ı�ֱ����ˮƽ����ļн�������ֱ����ˮƽ����ļн�Ϊ30��ʱ��СԲ����ֱ�����˶���ʱ����̣��������ٶ�Ϊg����(����)

A. ����F��СԲ���������ĺ���һ������ˮƽ�����30����б�����µķ���
B. ����Fһ������ˮƽ�����30����б�����µķ���
C. ������F�ķ���ˮƽ���ң������F�Ĵ�СΪ![]()
D. ����F����СֵΪ![]()
���𰸡�AD
��������A�����СԲ����ֱ�����˶���ʱ����̣������ٶȷ����ظ˵ķ�������F��СԲ���������ĺ���һ������ˮƽ�����30��б�����µķ���Ϊ�˵ķ���A��ȷ��
B��������⣬СԲ����ֱ�����˶���ʱ����̣�����ٶ���������������ĺ��������ظ˵ķ�����ô����F�ķ���ȷ������B����
C�Ҫʹʱ����̣�����ٶ��������F����غ��ַ���ȷ������F��mg�ĺ��������ظ����£�������F�ķ���ˮƽ���ң���ͼ��ʾ��������
����![]() ����C����
����C����
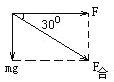
D�����F����mg��F�����ɹ���ʸ�������Σ�����ͼ��ʾ��
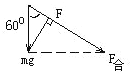
��ͼ��֪����F��F����ֱʱ������б�洹ֱʱ��F����С�����У�![]() ����D��ȷ��
����D��ȷ��
���磺���������������˶�������Ӧ�ã�����ţ�ٵڶ����ɵ����ݣ�����ʸ���ĺϳɷ���������֪ʶ�����ã�ע��ʱ����̣������ٶ��ظ˵ķ����ǽ����ͻ�ƿ���

 ������ÿ�ʱ��ҵϵ�д�
������ÿ�ʱ��ҵϵ�д�