Question

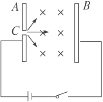
【题目】如图所示，一轻质弹簧的一端系一质量为m的小球，另一端固定在倾角为37°的光滑斜面体顶端，弹簧与斜面平行。在斜面体以大小为g的加速度水平向左做匀加速直线运动的过程中，小球始终相对于斜面静止。已知弹簧的劲度系数为k，则该过程中弹簧的形变量为(已知：sin 37°＝0.6，cos 37°＝0.8)(　　)

A. B.

C. D.

Answer 1

【答案】A

【解析】

以小球为研究对象，根据牛顿第二定律和胡克定律列式，求解弹簧的形变量。

在斜面体以大小为g的加速度水平向左做匀加速直线运动时，弹簧是处于伸长状态还是压缩状态，无法直接判断，此时可采用假设法，假设弹簧处于压缩状态，若求得弹力F为正值，则假设正确；水平方向上由牛顿第二定律得：FNsin θ＋Fcos θ＝mg　①；竖直方向上由受力平衡得：FNcos θ＝mg＋Fsin θ　②，①②联立得：F＝mg。由胡克定律得F＝kx，x＝，故选A。