Question

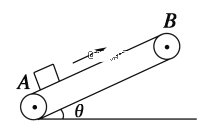
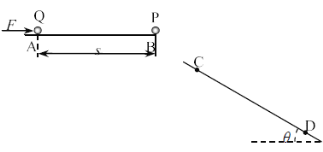
【题目】如图所示，B点为水平平台的最右端，平台右下方适当位置有一倾角的斜坡。质量M=300g的小球P静放在B点，小球Q静放在水平面上的A点，A、B的距离s=4.5m。小球Q在水平恒力F的作用下以a=4m/s2的加速度向右运动，当两小球接触前的瞬间撤去F，两球碰撞后球Q的动能减少为原来的四分之一，并刚好可以回到A点，球P落到斜坡上的C点，弹起后沿水平方向飞出，落到斜坡上的D点。若两球可视为质点，两球碰撞过程、球P与斜坡的碰撞过程中均没有能量损失，碰撞时间极短，重力加速度g取10m/s2，求：

（1）撤去F的瞬间，球Q的速度大小v0；

（2）力F的大小；

（3）C、D两点间的距离L。

Answer 1

【答案】（1）6m/s；（2）0.5N；（3）4.8m

【解析】

（1）由匀变速运动公式得

代入数据得

（2）设水平面对球Q的摩擦力大小为f，球Q的质量为m，球Q从A点运动到B点的过程中，由牛顿第二定律得：

F-f=ma

设两球碰撞后球Q、P的速度分别为v1、v2，由题意可知

取v0方向为正，两球碰撞过程由动量守恒定律得

由题意得

球Q从B点到A点的过程中，由动能定理得

联立各式并代入数据得

F=0.5N

（3）由题意可知，球P从斜坡上弹起速度与斜坡间的夹角为θ，由于碰撞过程没有能量损失且时间极短，故球P与斜坡碰撞前后速度大小相等，碰前速度方向与斜坡间的夹角也为θ

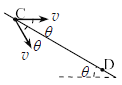
设球P落到C点的速度大小为v，球P从B点抛出，运动到C点，由平抛运动规律得

球P从C点弹起后以初速度v做平抛运动到达D点，由平抛运动规律得：

联立各式并代入数据得

L=4.8m