Question

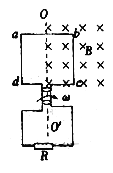
【题目】如图所示，边长为L=0.2m的正方形线圈abcd，其匝数为n=100、总电阻为r=2Ω，外电路的电阻为R=8Ω，ab的中点和cd的中点的连线OO′恰好位于匀强磁场的边界线上，磁场的磁感应强度B=1T，若线圈从图示位置开始，以角速度ω=2rad/s绕OO′轴匀速转动，则以下判断中正确的是

A. 在t=时刻，磁场穿过线圈的磁通量为0，故此时磁通量变化率为0

B. 闭合电路中感应电动势的瞬时表达式e=4sin2t(V)

C. 从t=0时刻到t=时刻，电阻R上产生的热量为Q=0.16πJ

D. 从t=0时刻到t=时刻，通过R的电荷量q=0.2C

Answer 1

【答案】BCD

【解析】

根据题中“磁场的…线圈从图示位置开始，以角速度ω=2rad/s绕OO′轴匀速转动”可知，本题考察交流电的产生问题，应用法拉第电磁感应定律、闭合电路欧姆定律、感应电量、有效值等知识分析计算。

A：在时刻，线圈从图示位置转过90°，磁场穿过线圈的磁通量为0，线圈中磁通量变化率最大。故A项错误。

B：线圈中产生感应电动势的最大值，开始计时时，线圈中磁通量最大，感应电动势为0，则闭合电路中感应电动势的瞬时表达式。故B项正确。

C：线圈转动的周期，回路中感应电流的最大值，回路中电流的有效值，从t=0时刻到时刻，电阻R上产生的热量。故C项正确。

D：从t=0时刻到时刻，电路中的平均感应电动势，电路中的平均电流，线框中磁通量的变化量，通过R的电荷量，解得：。故D项正确。