题目内容
1. 如图所示,小球在竖直放置的光滑圆形管道内做圆周运动,内侧壁半径为R,小球半径为r(略小于管道半径),则下列说法正确的是( )
如图所示,小球在竖直放置的光滑圆形管道内做圆周运动,内侧壁半径为R,小球半径为r(略小于管道半径),则下列说法正确的是( )| A. | 小球通过最高点时的最小速度vmin=$\sqrt{g(R+r)}$ | |
| B. | 小球通过最高点时的最小速度vmin=0 | |
| C. | 小球在水平线ab以下的管道中运动时,内侧管壁对小球一定无作用力 | |
| D. | 小球在水平线ab以上的管道中运动时,外侧管壁对小球一定有作用力 |
分析 小球在竖直光滑圆形管道内做圆周运动,在最高点,由于外管或内管都可以对小球产生弹力作用,从而可以确定在最高点的最小速度.小球做圆周运动时,沿半径方向的合力提供做圆周运动的向心力.根据牛顿第二定律求解管道对小球作用力大小和方向.
解答 解:A、B、由于管子能支撑小球,所以小球能够通过最高点时的最小速度为vmin=0;故A错误,B正确.
C、小球在水平线ab以下的管道中运动时,受到的合外力向上,则主要应是外侧管壁提供作用力,故内侧管壁对小球一定无作用力;故C正确;
D、小球在水平线ab以上的管道中运动时,外侧管壁对小球不一定有作用力.如速度较小时,重力与下管壁的合力充当向心力,故D错误.
故选:BC.
点评 本题考查向心力公式以及牛顿第二定律的应用,要注意圆管类似于杆模型,最高点可以提供支持力也可以提供向下的弹力,要根据物体的速度大小分析受力特点.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
12.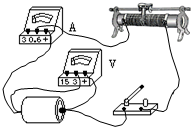 某同学用电流表和电压表测一节干电池的电动势和内电阻,所用滑动变阻器的阻值范围为0-20Ω,电路的实物图如图所示.该同学接线中错误和不规范的做法是( )
某同学用电流表和电压表测一节干电池的电动势和内电阻,所用滑动变阻器的阻值范围为0-20Ω,电路的实物图如图所示.该同学接线中错误和不规范的做法是( )
 某同学用电流表和电压表测一节干电池的电动势和内电阻,所用滑动变阻器的阻值范围为0-20Ω,电路的实物图如图所示.该同学接线中错误和不规范的做法是( )
某同学用电流表和电压表测一节干电池的电动势和内电阻,所用滑动变阻器的阻值范围为0-20Ω,电路的实物图如图所示.该同学接线中错误和不规范的做法是( )| A. | 滑动变阻器不起变阻作用 | B. | 电流表接线错误 | ||
| C. | 电压表量程选用不当 | D. | 电压表接线有错 |
9.如图甲所示是一种速度传感器的工作原理图,在这个系统中B为一个能发射超声波的固定小盒子,工作时小盒子B向被测物体发出短暂的超声波脉冲,脉冲被运动的物体反射后又被B盒接收,从B盒发射超声波开始计时,经时间△t0再次发射超声波脉冲,图乙是连续两次发射的超声波的位移-时间图象,则下列说法正确的是( )
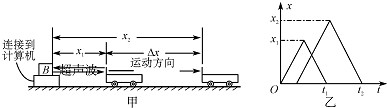

| A. | 超声波的速度为$\frac{2{x}_{1}}{{t}_{1}}$ | |
| B. | 物体的平均速度为$\frac{2({x}_{2}-{x}_{1})}{({t}_{2}-{t}_{1}+2△{t}_{0})}$ | |
| C. | 超声波的速度为$\frac{2{x}_{2}}{{t}_{2}}$ | |
| D. | 物体的平均速度为$\frac{2({x}_{2}-{x}_{1})}{({t}_{2}-{t}_{1}+△{t}_{0})}$ |
16.如图是做直线运动的甲、乙物体的位移-时间图象,由图象可知( )
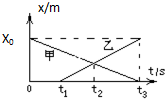

| A. | 甲起动的时间比乙早t1秒 | B. | t2时刻两物体相遇 | ||
| C. | t2时两物体相距最远 | D. | t3时两物体相距x0米 |
13.两个共点力的合力与分力的关系,以下说法中正确的是( )
| A. | 合力作用效果与两个分力共同作用的效果相同 | |
| B. | 合力与分力是同时存在的 | |
| C. | 合力的大小一定等于两个分力的大小之和 | |
| D. | 合力的大小可以小于它的任一个分力 |
10.在静电场中,下列有关电势能、电势判断错误的是( )
| A. | 电势能、电势都是仅有电场本身因素决定,与处于电场中的电荷无关 | |
| B. | 电势高的地方,电荷的电势能一定大 | |
| C. | 顺着电场线运动,电荷的电势能一定减少 | |
| D. | 某点电势的大小等于单位电荷在该点与在参考点的电势能差的大小 |
11. 在飞行跳伞表演中,某伞兵从静止的直升飞机上跳下,在t0时刻打开降落伞,在3t0时刻以速度v2着地.伞兵运动的速度随时间变化的规律如图所示.下列结论正确的是( )
在飞行跳伞表演中,某伞兵从静止的直升飞机上跳下,在t0时刻打开降落伞,在3t0时刻以速度v2着地.伞兵运动的速度随时间变化的规律如图所示.下列结论正确的是( )
 在飞行跳伞表演中,某伞兵从静止的直升飞机上跳下,在t0时刻打开降落伞,在3t0时刻以速度v2着地.伞兵运动的速度随时间变化的规律如图所示.下列结论正确的是( )
在飞行跳伞表演中,某伞兵从静止的直升飞机上跳下,在t0时刻打开降落伞,在3t0时刻以速度v2着地.伞兵运动的速度随时间变化的规律如图所示.下列结论正确的是( )| A. | 在0~t0时间内加速度不变,在t0~3t0时间内加速度减小 | |
| B. | 降落伞打开后,降落伞和伞兵所受的阻力越来越小 | |
| C. | 在t0~3t0的时间内,平均速度$\overline{v}$>$\frac{{v}_{1}+{v}_{2}}{2}$ | |
| D. | 若第一个伞兵在空中打开降落伞时第二个伞兵立即跳下,则他们在空中的距离先增大后减小,当两个伞兵下落速度相等时他们相距最远 |