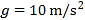题目内容
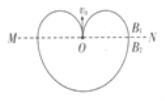
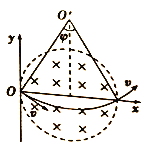
【题目】如图所示为圆形区域的匀强磁场，磁感应强度为B，方向垂直纸面向里，边界跟y轴相切于坐标原点O。O点处有一放射源，沿纸面向各方向射出速率均为v的某种带电粒子，带电粒子在磁场中做圆周运动的半径是圆形磁场区域半径的两倍。已知该带电粒子的质量为m、电荷量为q，不考虑带电粒子的重力。
(1)推导带电粒子在磁场空间做圆周运动的轨道半径。
(2)求带电粒子通过磁场空间的最大偏转角。
(3)沿磁场边界放置绝缘弹性挡板，使带电粒子与挡板碰撞后以原速率弹回，且其电荷量保持不变。若从O点沿x轴正方向射入磁场的粒子速度减小为0.5v，求该粒子第一次回到点经历的时间。
【答案】(1) 
； (2)60°； (3) 
；
【解析】(1)带电粒子进入磁场后，受洛伦兹力作用，设其做圆周运动的轨道半径为r，
由牛顿第二定律得： 
解得： 
(2)设粒子飞出和进入磁场的速度方向的夹角为
，
如图所示，则
，x是粒子在磁场中轨迹的两端点的直线距离。x最大值为2R，对应的就是
的最大值，且2R=r
所以
， 即
=60°
(3)当粒子的速度减小为
时，在磁场中做匀速圆周运动的半径
故粒子转过四分之一圆周，对应圆心角为
时与边界相撞并弹回，由对称性知粒子经过四个这样的过程后第一次回到O点，即经历时间为一个周期，粒子在磁场中做匀速圆周运动的周期
所以从O点沿x轴正方向射出的粒子第一次回到O点经历的时间是
【题目】某研究性学习小组在测量某电池电动势和内阻时，由于使用的是新电池，电池的内阻较小，为了防止在调节滑动变阻器时造成短路，电路中用一个定值电阻R0起保护作用．实验器材除电池、开关和导线外，还有：电流表(量程0.6A、3A)，电压表(量程3 V、15V)，定值电阻(阻值R0=1W)，滑动变阻器(阻值范围0～10W、额定电流2A)．
(1)该研究小组按照电路图正确连接好电路后进行实验，实验中移动滑动变阻器时，发现电流表示数变化明显，而电压表的示数变化不明显，引起该现象的主要原因是____________．
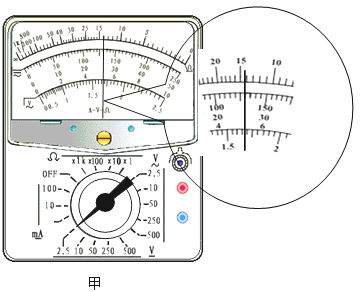
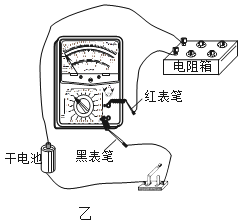
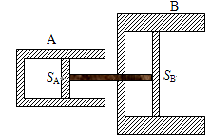
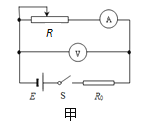
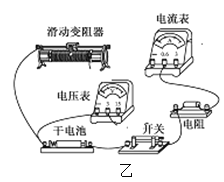
（2）该研究小组经过讨论，对电路进行了重新设计，根据设计好的电路图（如图甲）连接实际电路（如图乙），其中有两根导线未连接，请你帮助他连接好________________．
(3)调节滑动变阻器，电压表和电流表的示数记录如下：
U (V) | 1. 40 | 1. 30 | 1. 20 | 1. 10 | 1. 00 |
I (A) | 0.07 | 0. 15 | 0. 24 | 0. 32 | 0. 41 |
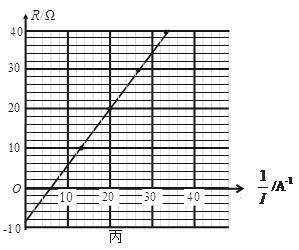
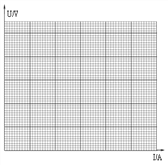
请根据表中的数据，在答题卡的方格纸上作出U－I 图线，____，并根据图线求得：电池电动势E =_______V；内阻r=________Ω．
(4)实验时该研究小组进行了多次测量，花费了较长时间，测量期间一直保持电路闭合．其实，从减小实验误差考虑，这样的操作不妥，其原因是__________（选择“A”或“B”）
A．通电时间较长引起电表损坏
B．通电时间较长导致电源发热，影响测量结果
