题目内容
4. 如图所示,某货场而将质量为m1=100kg的货物(可视为质点)从高处运送至地面,为避免货物与地面发生撞击,现利用固定于地面的光滑四分之一圆轨道,使货物中轨道顶端无初速滑下,轨道半径R=1.8m.地面上紧靠轨道次排放两声完全相同的木板A、B,长度均为l=2m,质量均为m2=100kg,木板上表面与轨道末端相切.货物与木板间的动摩擦因数为μ1,木板与地面间的动摩擦因数μ=0.2.(最大静摩擦力与滑动摩擦力大小相等,取g=10m/s2)
如图所示,某货场而将质量为m1=100kg的货物(可视为质点)从高处运送至地面,为避免货物与地面发生撞击,现利用固定于地面的光滑四分之一圆轨道,使货物中轨道顶端无初速滑下,轨道半径R=1.8m.地面上紧靠轨道次排放两声完全相同的木板A、B,长度均为l=2m,质量均为m2=100kg,木板上表面与轨道末端相切.货物与木板间的动摩擦因数为μ1,木板与地面间的动摩擦因数μ=0.2.(最大静摩擦力与滑动摩擦力大小相等,取g=10m/s2)(1)求货物到达圆轨道末端时对轨道的压力.
(2)若货物滑上木板A时,木板不动,而滑上木板B时,木板B开始滑动,求μ1应满足的条件.
(3)若μ1=0.5,求货物滑到木板A末端时的速度和在木板A上运动的时间.
分析 (1)物体下滑的过程中,机械能守恒,根据机械能守恒可以得出到达底端时的速度,再由向心力的公式可以求得物体受到的支持力的大小,根据牛顿第三定律可以得到货物到达圆轨道末端时对轨道的压力大小;
(2)货物滑上木板A时,木板不动,说明此时货物对木板的摩擦力小于地面对木板的摩擦力的大小,而滑上木板B时,木板B开始滑动,说明此时货物对木板的摩擦力大于了地面对货物的摩擦力的大小,由此可以判断摩擦因数的范围.
(3)当μ1=0.5时,由⑥式可知,货物在木板A上滑动时,木板不动,货物做的是匀减速直线运动,位移是木板的长度L,由匀变速直线运动的规律可以求得.
解答 解:(1)设货物滑到圆轨道末端是的速度为v0,对货物的下滑过程中根据机械能守恒定律得:$mgR=\frac{1}{2}{m_1}v_0^2$…①
设货物在轨道末端所受支持力的大小为FN,根据牛顿第二定律得:${F_N}-{m_1}g={m_1}\frac{v_0^2}{R}$…②
联立以上两式代入数据得:FN=3mg=3000N…③
根据牛顿第三定律,货物到达圆轨道末端时对轨道的压力大小为3000N,方向竖直向下.
(2)若滑上木板A时,木板不动,由受力分析得:μ1m1g≤μ2(m1+2m2)g…④
若滑上木板B时,木板B开始滑动,由受力分析得:μ1m1g>μ2(m1+m2)g…⑤
联立④⑤式代入数据得:0.4<μ≤0.6…⑥.
(3)μ1=0.5,由⑥式可知,货物在木板A上滑动时,木板不动.设货物在木板A上做减速运动时的加速度大小为a1,由牛顿第二定律得:
μ1m1g=m1a1 …⑦
设货物滑到木板A末端是的速度为v1,由运动学公式得:$v_1^2-v_0^2=-2{a_1}l$…⑧
联立①⑦⑧式代入数据得:v1=4m/s…⑨
设在木板A上运动的时间为t,由运动学公式得:
v1=v0-a1t…⑩
联立①⑦⑨⑩式代入数据得:t=0.4s.
答:(1)货物到达圆轨道末端时对轨道的压力是3000N;
(2)若货物滑上木板A时,木板不动,而滑上木板B时,木板B开始滑动,μ1应满足的条件是0.4<μ1≤0.6;
(3)若μ1=0.5,求货物滑到木板A末端时的速度和在木板A上运动的时间是0.4s.
点评 本题考查了机械能守恒、圆周运动和牛顿运动定律的应用,特别需要注意的是货物在水平面上运动时木板的运动状态,由于是两块木板,所以货物运到到不同的地方时木板的受力不一样.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 通过C点时速度大小为3m/s | |
| B. | BC段位移为12m | |
| C. | 第5s末的速度大小为2m/s | |
| D. | 汽车在AC段平均速度大于CB段平均速度 |
| A. | “天宫一号”飞行器的高度要略调高一点 | |
| B. | 地球赤道上物体的重力会略变大 | |
| C. | 同步卫星的高度要略调低一点 | |
| D. | 地球的第一宇宙速度将略变小 |
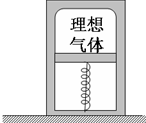 如图所示,密闭绝热的具有一定质量的活塞,活塞的上部封闭着气体,下部为真空,活塞与器壁的摩擦忽略不计,置于真空中的轻弹簧的一端固定于理想气体容器的底部.另一端固定在活塞上,弹簧被压缩后用绳扎紧,此时弹簧的弹性势能为EP(弹簧处于自然长度时的弹性势能为零),现绳突然断开,弹簧推动活塞向上运动,经过多次往复运动后活塞静止,气体达到平衡态,经过此过程( )
如图所示,密闭绝热的具有一定质量的活塞,活塞的上部封闭着气体,下部为真空,活塞与器壁的摩擦忽略不计,置于真空中的轻弹簧的一端固定于理想气体容器的底部.另一端固定在活塞上,弹簧被压缩后用绳扎紧,此时弹簧的弹性势能为EP(弹簧处于自然长度时的弹性势能为零),现绳突然断开,弹簧推动活塞向上运动,经过多次往复运动后活塞静止,气体达到平衡态,经过此过程( )| A. | EP全部转换为气体的内能 | |
| B. | EP一部分转换成活塞的重力势能,其余部分仍为弹簧的弹性势能 | |
| C. | EP全部转换成活塞的重力势能和气体的内能 | |
| D. | EP一部分转换成活塞的重力势能,一部分转换为气体的内能,其余部分仍为弹簧的弹性势能 |
 我们在生活中移动货物经常推着或拉着物体沿地面运动,这样方便省力.在粗糙的水平面上放置一个小物体P.P受到与水平面成夹角θ、斜向上的拉力F作用沿水平面运动,如图甲所示,物体P的加速度随F变化规律如图乙中图线P所示.把物体P换成Q,其他条件不变,重复操作,得到Q的加速度随F变化规律如图乙中图线Q所示.图乙中b,c和d都是已知量,由此可知( )
我们在生活中移动货物经常推着或拉着物体沿地面运动,这样方便省力.在粗糙的水平面上放置一个小物体P.P受到与水平面成夹角θ、斜向上的拉力F作用沿水平面运动,如图甲所示,物体P的加速度随F变化规律如图乙中图线P所示.把物体P换成Q,其他条件不变,重复操作,得到Q的加速度随F变化规律如图乙中图线Q所示.图乙中b,c和d都是已知量,由此可知( )| A. | P和Q的材料相同 | B. | P的质量大于Q的质量 | ||
| C. | P的质量为$\frac{d}{b}$ | D. | Q的质量为-$\frac{c}{d}$ |
 断开含变压器、电动机等设备的电路的开关时,开关中的金属片之间会产生电火花,电火花会烧蚀接触点,甚至引起人身伤害.关于电火花产生的原因,以下说法正确的是( )
断开含变压器、电动机等设备的电路的开关时,开关中的金属片之间会产生电火花,电火花会烧蚀接触点,甚至引起人身伤害.关于电火花产生的原因,以下说法正确的是( )| A. | 断开时金属片之间摩擦起电 | |
| B. | 断开时设备中的线圈产生很大的感应电动势 | |
| C. | 由于设备正常工作时的电压很大引起的 | |
| D. | D由于设备正常工作时的电流很大引起的 |

