Question

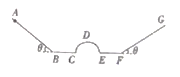
【题目】如图所示，固定在竖直平面内的轨道由硬杆制成，其中水平轨道BC和EF的长度均为2R．AB、FG部分的倾角均为＝，CDE部分是半径为R的半圆轨道，B、C、E、F四点共线且各部分均平滑连接，将一个质量为m的圆环套在轨道上从A点由静止释放，已知AB＝6R，小环与BC和EF间的动摩擦因数均为＝0．1，轨道其他部分均光滑，重力加速度为g，求：

（1）小环从释放至第一次到达B点所用的时间

（2）小环第一次向右通过半圆執道的最高点D时，对轨道的作用力

（3）小环通过半圆轨道的最高点D的次数及其最终停在轨道上的位置

Answer 1

【答案】（1）；（2）2.6mg；（3）7次，E点

【解析】

(1)根据牛顿第二定律得，小环沿AB下滑的加速度a=mgsinθ/m=gsinθ=g/2，

根据6R=at2得，小环从释放第一次到达B点的时间t=.

(2)对A到D段运用动能定理得,mg(6RsinθR)μmg2R=0，

在最高点D，根据牛顿第二定律得,mg+F=，

解得F=2.6mg.

(3)对全过程运用动能定理得，mg6Rsinθμmgs=0，

解得s=30R.

n==7.5，可知小环通过最高点D的次数为7次，最后停在E处。