Question

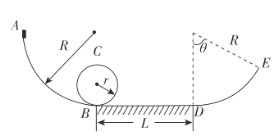
【题目】如图为过山车的简化模型，AB是一段光滑的半径为R的四分之一圆弧轨道，B点处接一个半径为r的竖直光滑圆轨道，滑块从圆轨道滑下后进入一段长度为L的粗糙水平直轨道BD，最后滑上半径为R，圆心角θ=60°的光滑圆弧轨道DE。现将质量为m的滑块从A点由静止释放，求∶

(1)若R=3r，求滑块第一次到达竖直圆轨道最高点时对轨道的压力大小；

(2)若要求滑块能滑上DE圆弧轨道但不会从E点冲出轨道，并最终停在平直轨道上，平直轨道BD的动摩擦因数μ需满足的条件。

Answer 1

【答案】(1)；(2)

【解析】

(1)对滑块，从A到C的过程，由机械能守恒可得：

根据牛顿第二定律

代入，得

由牛顿第三定律得

(2)滑块由A到B得

若滑块恰好停在D点，从B到D的过程，由动能定理可得：

可得

若滑块恰好不会从E点冲出轨道，从B到E的过程，由动能定理可得：

可得

综上所述，需满足的条件为