题目内容
(10分)在真空中有一正方体玻璃砖,其截面如图所示,已知它的边长为d.在AB面上方有一单色点光源S,从S发出的光线SP以60°入射角从AB面中点射入,当它从侧面AD射出时,出射光线偏离入射光线SP的偏向角为30°,若光从光源S到AB面上P点的传播时间和它在玻璃砖中传播的时间相等,求点光源S到P点的距离。


L= d(
d(
 d(
d(试题分析:(10分)光路图如图所示,由折射定律知,光线在AB面上折射时有n=
 (1分)
(1分)在BC面上出射时n=
 (1分)
(1分)
由几何关系有
 +β=90°(1分)
+β=90°(1分)δ=(60°-
 )+(γ-β)=30°(1分)
)+(γ-β)=30°(1分)联立以上各式并代入数据解得
 =β=45°,γ=60°(1分)
=β=45°,γ=60°(1分)所以n=
 (1分)
(1分)光在棱镜中通过的距离s=
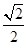 d=
d= t(2分)
t(2分)设点光源到P点的距离为L,有L=ct(1分)
解得L=
 d(1分)
d(1分)
练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
 ,BC边长为2L,该介质的折射率为
,BC边长为2L,该介质的折射率为 。求:
。求: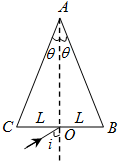
 或
或 )。
)。 点,
点, 垂直底边,下列说法正确的是( )
垂直底边,下列说法正确的是( )
 .MN是一条通过球心的直线,单色细光束AB平行于MN射向球体,B为入射点,AB与MN间距为5
.MN是一条通过球心的直线,单色细光束AB平行于MN射向球体,B为入射点,AB与MN间距为5
 .求:
.求:

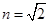 。在此截面所在的平面内,一条光线以45o的入射角从AC边的中点M射入棱镜(如图所示)。画出光路图,并求光线从棱镜射出的点的位置(不考虑光线沿原来路返回的情况)。
。在此截面所在的平面内,一条光线以45o的入射角从AC边的中点M射入棱镜(如图所示)。画出光路图,并求光线从棱镜射出的点的位置(不考虑光线沿原来路返回的情况)。


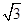
 (即:
(即: ),求:
),求: