题目内容
 宇航员站在一星球表面上,沿水平方向以初速度v0从倾斜角为θ的斜面顶端P处抛出一个小球,测得经过时间t小球落在斜面上的另一点Q,已知该星球的半径为R,求:
宇航员站在一星球表面上,沿水平方向以初速度v0从倾斜角为θ的斜面顶端P处抛出一个小球,测得经过时间t小球落在斜面上的另一点Q,已知该星球的半径为R,求:(1)该星球表面的重力加速度;
(2)该星球的第一宇宙速度.
分析:(1)小球做平抛运动,水平位移x=υ0t,竖直位移y=
gt2,再根据几何关系即可求得该星球表面的重力加速度g;
(2)该星球的近地卫星的向心力由万有引力提供,该星球表面物体所受重力等于万有引力,联立方程即可求出该星球的第一宇宙速度υ;
| 1 |
| 2 |
(2)该星球的近地卫星的向心力由万有引力提供,该星球表面物体所受重力等于万有引力,联立方程即可求出该星球的第一宇宙速度υ;
解答: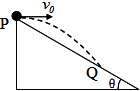 解:(1)小球从P到Q的过程中由平抛运动规律得:
解:(1)小球从P到Q的过程中由平抛运动规律得:
水平位移x=υ0t,竖直位移y=
gt2
由位移关系得:tanθ=
=
,
解得:g=
(2)该星球的近地卫星的向心力由万有引力提供
G
=m
①
该星球表面物体所受重力等于万有引力,
G
=mg②
由①②得v=
=
答:(1)该星球表面的重力加速度为
;
(2)该星球的第一宇宙速度为
.
 解:(1)小球从P到Q的过程中由平抛运动规律得:
解:(1)小球从P到Q的过程中由平抛运动规律得:水平位移x=υ0t,竖直位移y=
| 1 |
| 2 |
由位移关系得:tanθ=
| y |
| x |
| ||
| v0t |
解得:g=
| 2v0tanθ |
| t |
(2)该星球的近地卫星的向心力由万有引力提供
G
| Mm |
| R2 |
| v2 |
| R |
该星球表面物体所受重力等于万有引力,
G
| Mm |
| R2 |
由①②得v=
| gR |
|
答:(1)该星球表面的重力加速度为
| 2v0tanθ |
| t |
(2)该星球的第一宇宙速度为
|
点评:该题主要考查了平抛运动及圆周运动的相关知识,要求同学们能熟练掌握平抛运动的基本公式及向心力公式,难度适中.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目