题目内容
宇航员站在一星球表面上的某高处,将一小球以初速度v0做平抛运动,经过时间t,小球落到星球表面,测得抛出点与落地点之间的距离为L,
(1)求该星球表面的重力加速度g?
(2)若该星球的半径为R,万有引力常量为G,求该星球的质量M?
(1)求该星球表面的重力加速度g?
(2)若该星球的半径为R,万有引力常量为G,求该星球的质量M?
分析:(1)平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,结合平抛运动的规律求出星球表面的重力加速度.
(2)根据万有引力等于重力求出星球的质量.
(2)根据万有引力等于重力求出星球的质量.
解答:解:(1)如图所示,设抛出点的高度为h,平抛运动的水平射程为x,则有: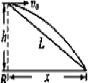
x2+h2=L,其中x=v0t,
则有:(v0t)2+h2=L2.
由此解得h=
.
设该星球表面的重力加速度为g,根据h=
gt2得,
g=
=
.
(2)根据G
=mg得,
M=
=
.
答:(1)星球表面的重力加速度为
.
(2)星球的质量为
.

x2+h2=L,其中x=v0t,
则有:(v0t)2+h2=L2.
由此解得h=
| L2-(v0t)2 |
设该星球表面的重力加速度为g,根据h=
| 1 |
| 2 |
g=
| 2h |
| t2 |
2
| ||
| t2 |
(2)根据G
| Mm |
| R2 |
M=
| gR2 |
| G |
2
| ||
| Gt2 |
答:(1)星球表面的重力加速度为
2
| ||
| t2 |
(2)星球的质量为
2
| ||
| Gt2 |
点评:解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,以及掌握万有引力等于重力这一理论,并能灵活运用.

练习册系列答案
相关题目