题目内容
（12分）如图所示，倾角为30°的光滑斜面的下端有一水平传送带，传送带正以6 m/s的速度运动，运动方向如图所示．一个质量为2 kg的物体(物体可以视为质点)，从h＝3.2 m高处由静止沿斜面下滑，物体经过A点时，不管是从斜面到传送带还是从传送带到斜面，都不计其动能损失．物体与传送带间的动摩擦因数为0.5，物体向左最多能滑到传送带左右两端AB的中点处，重力加速度g＝10 m/s2，则：
(1)物体由静止沿斜面下滑到斜面末端需要多长时间？
(2)传送带左右两端AB间的距离l至少为多少？
(3)上述过程中物体与传送带组成的系统产生的摩擦热为多少？
【答案】
(1) 1.6s (2) 12.8m (3) 160J
【解析】
试题分析：（12分）(1)物体在斜面上由牛顿第二定律得：
mgsinθ＝ma， （1分）
＝
，
（1分）
可得t＝1.6 s. （2分）
(2)由能的转化和守恒得：
， （2分）
l＝12.8 m. （2分）
(3)此过程中，物体与传送带间的相对位移
，
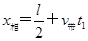（1分）
又
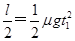（1分）
而摩擦热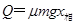
，
（1分）
以上三式可联立得Q＝160 J. （1分）
考点：功能关系
点评：难题。在有摩擦力或介质阻力参与的过程中，机械能不停地向内能转化，但在摩擦力或介质阻力大小不变的情况下，损失的机械能与通过的路程成正比．
练习册系列答案
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
黄冈360度定制密卷系列答案
阳光考场单元测试卷系列答案
相关题目
如图所示，倾角为30°的光滑斜面静止在水平地面上，斜面上放一质量为2kg的小球，球被垂直于斜面的固定挡板挡住而处于静止状态，g取10m/s2．
如图所示，倾角为30°的斜面体固定在水平地面上，一根不可伸长的轻绳两端分别系着小球A和物块B，跨过固定于斜面体顶端的滑轮O（可视为质点）．A的质量为m，B的质量为4m．开始时，用手托住A，使OA段绳恰处于水平伸直状态（绳中无拉力），OB绳平行于斜面，此时B静止不动．将A由静止释放，在其下摆过程中B始终保持静止．则在绳子到达竖直位置之前，下列说法正确的是（ ）
如图所示，倾角为θ=30°的斜面固定于水平地面上，在斜面底端0处固定有一轻弹簧，斜面顶端足够高．斜面上OM段光滑，M点的以上均粗糙．质量为m的物块A在M点恰好能静止，在离M点的距离为L的N点处，有一质量为2m的光滑物块B以速度V0=
（2008?武昌区模拟）如图所示，倾角为θ=30°的光滑绝缘斜面处于电场中，斜面AB长为L，一带电量为+q、质量为m的小球，以初速度υ0由斜面底端的A点开始沿斜面上滑，到达斜面顶端的速度仍为υ0，则（ ）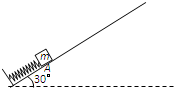
（2009?盐城一模）如图所示，倾角为30°的光滑斜面，底端固定一沿斜面方向的弹簧．一质量为m的滑块将弹簧压缩到A点（滑块与弹簧不连接），此时弹簧的压缩量为△L．滑块在A点由静止释放，沿斜面滑过距离L时速度为0．求：