题目内容
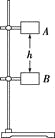
【题目】如图所示,一根不计质量的轻杆AC垂直插入竖直墙内,杆的另一端装一质量不计的光滑小滑轮,一根轻细绳BCD跨过滑轮,绳子B端固定在墙上,且BC段与墙之间的夹角为60°,CD段竖直且足够长.一质量为![]() 带孔的小球穿在细绳CD段上,小球以加速度
带孔的小球穿在细绳CD段上,小球以加速度![]() 匀加速下滑,不计空气阻力,
匀加速下滑,不计空气阻力,![]() .则滑轮对轻杆的作用力大小为
.则滑轮对轻杆的作用力大小为

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
先根据牛顿第二定律求解绳子的拉力,然后将绳子的拉力进行合成,得到绳子对滑轮的压力,然后对滑轮分析,根据共点力平衡条件得到杆对滑轮的作用力大小.
对小球,由牛顿第二定律:mg-T=ma,解得T=8N,故绳子的张力T=8N;将绳子的拉力进行合成,如图所示: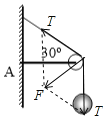
故绳子对滑轮的压力为T=8N;滑轮受绳子的压力和杆的支持力而平衡,故杆对滑轮的作用力大小为8N,由牛顿第三定律可知滑轮对轻杆的作用力大小为8N,故B正确;故选B。

练习册系列答案
相关题目
【题目】下表是某同学为探究弹力和弹簧伸长的关系所测的几组数据:
弹力F/N | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 |
弹簧的伸长量x/cm | 2.6 | 5.0 | 6.8 | 9.8 | 12.4 |
(1)请你在图中的坐标线上作出F-x图象.

(2)写出曲线所代表的函数.(x用m作单位)
(3)解释函数表达式中常数的物理意义.