��Ŀ����
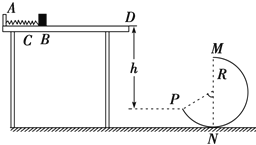
����Ŀ����ͼ��ʾ��ˮƽ��������һ�ᵯ�ɣ���˹̶���A�㣬��Ȼ״̬ʱ���Ҷ�λ��B�㣮ˮƽ�����Ҳ���һ��ֱ���õĹ��MNP������״Ϊ�뾶R=1.0m��Բ����ȥ�����Ͻ�120���Բ����MNΪ����ֱֱ����P�㵽�������ֱ������h=2.4m��������Ϊm=0.2kg����齫���ɻ���ѹ�����ͷţ���龭��B��������������ȱ����˶�����λ����ʱ��Ĺ�ϵΪx=6t��2t2�������������ǡ����P������������Բ����������ƿ���������gȡl0m/s2��
��1��������B��ʱ��˲ʱ�ٶȴ�СvB������������Ķ�Ħ�������̣�
��2�������պ��ܵ�������ߵ�M��������P�㵽M���˶������п˷�Ħ���������Ĺ�W��
���𰸡���1��6m/s��0.4����2��2.4J��
����������1������B������ȱ����˶�����x=6t��2t2֪��vB=6m/s
a=4m/s2
��ţ�ٵڶ����ɣ���mg=ma
��æ�=0.4
��2������պ��ܵ���M�㣬��![]()
��ƽ���˶����ɣ���P����ֱ���� ![]()
���ԣ�vy=vPsin60��
��P��M�Ĺ��̣��ɶ��ܶ�����![]()
�������W=2.4J��

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ