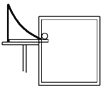
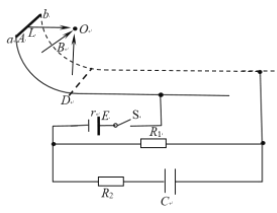
[题目]如图所示.一可视为质点的小球以初速度v0从O点水平抛出.经与两墙壁七次碰撞后刚好落在竖直墙壁的最低点D.此时速度与水平方向的夹角为θ.其中A .C两点为小球与另一墙壁碰撞的等高点.已知两墙壁间的距离为d.与墙壁碰撞无能量损失.且速度满足光的反射规律.则下列说法正确的是A. xOA:xAB:xBC:xCD＝1:3:5:7B. 相邻两点间的速度的变化量均题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图所示，一可视为质点的小球以初速度v0从O点水平抛出，经与两墙壁七次碰撞后刚好落在竖直墙壁的最低点D，此时速度与水平方向的夹角为θ，其中A 、C两点为小球与另一墙壁碰撞的等高点，已知两墙壁间的距离为d，与墙壁碰撞无能量损失，且速度满足光的反射规律，则下列说法正确的是

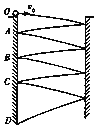
A. xOA：xAB：xBC：xCD＝1：3：5：7

B. 相邻两点间的速度的变化量均不相等；

C. tanθ＝

D. tanθ＝

【答案】AC

【解析】

A. 小球在水平方向上速度的大小相等，根据等时性知，OA、AB、BC、CD时间相等，在竖直方向上做自由落体运动，根据初速度为零的匀变速直线运动的推论，知xOA：xAB：xBC：xCD＝1：3：5：7.故A正确；

B. 因为在相邻两点间所需的时间相等，水平方向上的速度大小不变，竖直方向上做自由落体运动，根据△v=gt，则相邻两点间的速度变化量相等。故B错误；

C.D. 小球从O点运动到D点的时间t=，则tanθ=.故C正确，D错误。

故选：AC.

练习册系列答案

（1）穿过线圈的磁通量是如何变化的？

（2）线圈中的感应电动势为多大？

（3）若上述过程所经历的时间为0.1s，线圈中产生的感应电动势为20V，则线圈中的磁通量变化了多少？

【题目】如图甲，位于M板处的粒子源可以不断产生初速度为零的电子，电子在MN板间被加速，在MN板间所加电压按图乙所示规律变化。，电子射出后从坐标原点O进入x轴上方一垂直纸面向外的有界匀强磁场区域．发生270°偏转后沿y轴负方向射出有界磁场打到x轴下方水平放置的荧光屏上。N板到y轴、荧光屏到x轴的距离均为L。已知电子的质量为m，电量为－e(e>0)，磁场的磁感应强度大小为B。忽略电子在板间被加速的时间，认为电子在MN板间运动过程中板间电压不变，不考虑电子运动过程中的相互作用。求：

(1)t=0时刻从N板射出的电子在磁场中运动的半径大小；

(2)电子在t=0时刻从N板射出到打到荧光屏所经历的时间；

(3)为使0—2t0时间内从MN板间射出的电子均能发生270°偏转垂直打在荧光屏上，试求所加磁场区域的最小面积。

【题目】肩负着“落月”和“勘察”重任的“嫦娥三号”沿地月转移轨道直奔月球，如图所示，在距月球表面100 km的P点进行第一次制动后被月球捕获，进入椭圆轨道Ⅰ绕月飞行，之后，卫星在P点又经过第二次“刹车制动”，进入距月球表面100 km的圆形工作轨道Ⅱ，绕月球做匀速圆周运动，在经过P点时会再一次“刹车制动”进入近月点距月球表面15公里的椭圆轨道Ⅲ，然后择机在近月点下降进行软着陆，则下列说法正确的是(　　)

A. “嫦娥三号”在轨道Ⅰ上运动的周期最长

B. “嫦娥三号”在轨道Ⅲ上运动的周期最长

C. “嫦娥三号”经过P点时在轨道Ⅰ上运动的线速度最大

D. “嫦娥三号”经过P点时，在三个轨道上的加速度相等

【题目】如图所示，电源电动势为E，内电阻为r，理想电压表V1、V2示数为U1、U2，其变化量的绝对值分别为ΔU1和ΔU2；流过电源的电流为I，其变化量的绝对值为ΔI。在滑动变阻器的触片从右端滑到左端的过程中(灯泡电阻不变化)(　　)

A. 小灯泡L1、L3变暗，L2变亮

B. ΔU1＞ΔU2

C. 增大

D. 不变

【题目】(1)在“研究平抛运动”的实验中，可以描绘平抛物体运动轨迹和求物体的平抛初速度.实验简要步骤如下：

A.让小钢球多次从________位置上滚下，记下小球运动途中经过的一系列位置；

B.安装好器材，注意斜槽末端水平和木板竖直，记下小球在斜槽末端时球心在木板上的投影点O和过O点的竖直线，检测斜槽末端水平的方法是________________________________；

C.测出曲线上某点的坐标x、y，用v0＝________算出该小球的平抛初速度，实验需要对多个点求v0的值，然后求它们的平均值；

D.取下白纸，以O为原点，以竖直线为y轴建立坐标系，用平滑曲线画平抛轨迹.

上述实验步骤的合理顺序是________(只排列序号即可).

(2)在另一次实验中将白纸换成方格纸，每小格的边长L＝5 cm，通过实验，记录了小球在运动途中的三个位置，如图所示，则该小球做平抛运动的初速度为_____m/s；B点的竖直分速度为____m/s.(g取10 m/s2)

【题目】某高中物理课程基地拟采购一种能帮助学生对电偏转和磁偏转理解的实验器材该器材的核心结构原理可简化为如图所示一匀强电场方向竖直向下，以竖直线ab、cd为边界，其宽度为L，电场强度的大小为在cd的左侧有一与cd相切于N点的圆形有界匀强磁场，磁场的方向垂直纸面、水平向外现有一质量为m，电荷量为q的带正电粒子自O点以水平初速度正对M点进入该电场后，从N点飞离cd边界，再经磁场偏转后又从P点垂直于cd边界回到电场区域，并恰能返回O点粒子重力不计试求：