Question

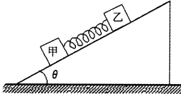
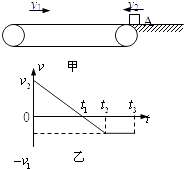
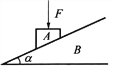
【题目】如图甲所示，斜面体固定在粗糙的水平地面上，底端与水平面平滑连接，一个可视为质点的物块从斜面体的顶端自由释放，其速率随时间变化的图象如图乙所示，（已知斜面与物块、地面与物块的动摩擦因数相同，g取10m/s2）求：

（1）斜面的长度S；
（2）物块与水平面间的动摩擦因数μ；
（3）斜面的倾角θ的正弦值．

Answer 1

【答案】
（1）解：由题意可知，物体在斜面上做匀加速直线运动，后在水平面上做匀减速直线运动，

速度时间图象与时间轴围成的面积表示位移，则斜面的长度为：S=

答：斜面的长度S为25m

（2）解：在水平面上做匀减速直线运动的加速度为：

根据牛顿第二定律得：﹣μmg=ma1

解得：

答：物块与水平面间的动摩擦因数μ为0.5

（3）解：物体在斜面上做匀加速直线运动的加速度为：

根据牛顿第二定律得：

mgsinθ﹣μmgcosθ=ma2

又因为（sinθ）2+（cosθ）2=1

解得：sinθ=0.29

答：斜面的倾角θ的正弦值为0.29

【解析】（1）物块先在斜面上做匀加速，后在粗糙水平面上做匀减速．由图象可知匀加速的时间与最大速度，从而可求出斜面的长度；（2）由图象可知匀减速的时间与速度变化，从而求出加速度的大小，最终由牛顿第二定律求出物体与水平面的动摩擦因数；（3）根据图象求出匀加速运动的加速度，根据牛顿第二定律求出斜面的倾角θ的正弦值．
【考点精析】根据题目的已知条件，利用V-t图象的相关知识可以得到问题的答案，需要掌握v-t图像：①在速度图像中，可以读出物体在任何时刻的速度；②在速度图像中，物体在一段时间内的位移大小等于物体的速度图像与这段时间轴所围面积的值；③在速度图像中，物体在任意时刻的加速度就是速度图像上所对应的点的切线的斜率；④图线与横轴交叉，表示物体运动的速度反向；⑤图线是直线表示物体做匀变速直线运动或匀速直线运动;图线是曲线表示物体做变加速运动．